Question 1099636: Alice has saved 5.00 in dimes, quarters, and half dollars. She finds that she has 30 coins altogether and there are four times as many quarters as there are half dollars. How many dimes does Alice have ?
Found 4 solutions by josgarithmetic, ankor@dixie-net.com, ikleyn, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! d = no. dime; q = no. of quarters; h = no. of half dollars
:
Write an equation for each statement
:
Alice has saved 5.00 in dimes, quarters, and half dollars.
.10d + .25q + .50h = 5.00
:
She finds that she has 30 coins altogether
d + q + h = 30
:
there are four times as many quarters as there are half dollars.
q = 4h
In the 2nd equation, replace q with 4h
d + 4h + h = 30
d + 5h = 30
d = (30-5h)
In the 1st equation replace d with (30-5h)
.10(30-5h) + .25q + .50h = 5.00
3 - .5h + .25q + .50h = 5.00
.50h - .50h + .25h = 5 - 3
.25q = 2
q = 2/.25
q = 8 quarters
:
In the equation d + q + q = 30, replace q with 8
d + 8 + h = 30
d + h = 30 - 8
d + h = 22
Replace d = (30-5h)
30 - 5h + h = 22
-5h + h = 22 - 30
-4h = -8
h = -8/-4
h = 2 half dollars
Find d
d + 2 = 22
d = 22 - 2
d = 20 dimes
How many dimes does Alice have ?
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
Alice has saved 5.00 in dimes, quarters, and half dollars. She finds that she has 30 coins altogether and
there are four times as many quarters as there are half dollars. How many dimes does Alice have ?
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let solve it IN FEW LINES.
Let H be the number of half-dollars.
Then the number of quarters is 4H, according to the condition.
Hence, the dimes are the rest (30-H-4H) = (30-5H) coins.
The dimes contribute 10*(30-5H) cents towards to the total.
The quarters contribute 25*((4H) = 100H cents towards to the total.
Finally, the half-dollars contribute 50*H cents towards to the total.
Thus the total is 10*(30-5H) + 100H + 50H,
and your money equation is
10*(30-5H) + 100H + 50H = 500 cents. (Should I explain that $5 is 500 cents ?)
This is the simple equation in one unknown. Let's solve it together.
300 - 50H + 100H + 50H = 500 ====> 100H = 500 - 300 = 200 ====> H = 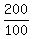 = 2.
So, there are 2 half-dollar coins, 4*2 = 8 quarters, and the rest 30-2-8 = 20 coins are dimes.
Let us CHECK the solution: 20*10 + 8*25 + 50*2 = 500 cents. ! Correct !
Solved.
It is a simple problem, and it should be solved as simple as possible.
-------------------
There is entire bunch of lessons on coin problems
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Kevin and Randy Muise have a jar containing coins
- Typical coin problems from the archive
- Three methods for solving standard (typical) coin word problems
- More complicated coin problems
- Solving coin problems mentally by grouping without using equations
- Santa Claus helps solving coin problem
- OVERVIEW of lessons on coin word problems
in this site.
You will find there the lessons for all levels - from introductory to advanced,
and for all methods used - from one equation to two equations and even without equations.
Read them and become an expert in solution of coin problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Coin problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by MathTherapy(10552)  (Show Source):
|
|
|
