Question 10994: Find three consecutive even integers such that twice the smaller is 26 less than 3 times the larger.
Answer by kinupanda(9)   (Show Source): (Show Source):
You can put this solution on YOUR website! We need to find three integers. For simplicity, let's define the smallest of these three as  . Similarly, because we know that all the integers are even, we can define the middle number as two more than the first; thus, . Similarly, because we know that all the integers are even, we can define the middle number as two more than the first; thus,  . The largest is 2 greater than that one; thus, it equals . The largest is 2 greater than that one; thus, it equals 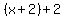 , which is equal to , which is equal to  . So, in our notation, the three numbers, from smallest to largest, will be . So, in our notation, the three numbers, from smallest to largest, will be  , ,  , and , and  . .
We need to take our expressions and apply the other information to it now. "Twice the smaller is 26 less than 3 times the larger," it says. In other words, we have  . .
To solve this equation, we can substitute our expressions for the numbers into it. From above, the smallest and largest numbers are  and and  , respectively. So we get: , respectively. So we get:

 ... distribute the 3 on the right ... distribute the 3 on the right
 ... combine like terms on the right ... combine like terms on the right
 ... subtract 3x from both sides ... subtract 3x from both sides
 ... divide both sides by -1 ... divide both sides by -1
Thus, we get  . Because this is the smallest of three consecutive even integers, we can conclude immediate that the other numbers we need are 16 and 18. Alternatively, we could substitute back into our expressions: if we substitute . Because this is the smallest of three consecutive even integers, we can conclude immediate that the other numbers we need are 16 and 18. Alternatively, we could substitute back into our expressions: if we substitute  , then we get , then we get  and and  . Thus, our solution is the numbers 14, 16, and 18. . Thus, our solution is the numbers 14, 16, and 18.
To check, we just see if twice the smaller is 26 less than three times the larger. So, twice the smaller is  . Three times the larger is . Three times the larger is  . .  , which is what it should be. Thus, our solution is valid! , which is what it should be. Thus, our solution is valid!
|
|
|