Question 1099331: Hi,
Please help me solve this question.
a is an acute angle such that sin a =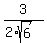 
By sketching a right angled triangle, show that tan a =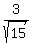 
How do I do this when I don't have a side length to work out the angle with trigonometry? Please help me! I'm so confused.
Found 2 solutions by josmiceli, KMST:
Answer by josmiceli(19441)   (Show Source):
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! The word "sketch" suggests that you would just draw something as an illustration,
without caring for accuracy or straightness of the lines,
maybe labeling vertices,
and based on the drawing would use your knowledge of trigonometry,
and of the Pythagorean theorem to calculate
what the values of the trigonometric ratio would be
for an ideal triangle where  exactly.
It could be something like this:
 The angles of that drawing are not such that ,
but we say it is just a "sketch" representing the problem.
Then you could say that your triangle has BC and AB side lengths
(no need to mentions units or measure sides)
that yield ,
such as  and  .
With the numbers above, you could calculate AC.
The Pythagorean theorem says that  ,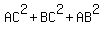
so 
 .
Then, 
You could also just state that  ,
and work the same calculations without specific length.
It just gets to be more cumbersome.
There is an infinite number of similar right triangles that have .
They all look like scaled up or scale down versions of one another, and they all have the same  .
Saying that the one you sketched has and
is good enough for a proof in my book.
The wording of the question sounds like you are expected to draw a right triangle ABC
such that ,
measure its legs, and calculate the tangent of A as a ratio of leg lengths.
I do not hink that is what was meant.
Doing an exact drawing without using the fact that is a bit tricky,
but I will show you what your knowledge of geometry can do for you.
First you must decide how large to make your triangle.
There is an infinite number of similar right triangles that have .
They all look like scaled up or scale down versions of one another, and they all have the same .
Let's say you deice that the hypotenuse of your right triangle will measure 100mm.
Draw a line, set your compass for a circle of radius  ,
and draw an arc that crosses your line at two points, A and B, like this
 Now, set the compass for an arc of radius  ,
and draw a small arc centered at B that crosses the arc you made before.
The point where the arcs cross is point C, with  .
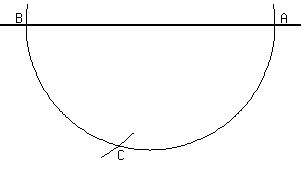 Connect point C to points A and B to get your right triangle.
The reason this works is because
1) an inscribed angle that intercepts a semicircle is always a right angle, and
2)we made AB and BC such that  was the value we needed for  .
|
|
|
