SOLUTION: please could you verify this? {{{(tan(5x/2))/(tan(x/2)) = (sin3x+sin2x)/(sin3x-sin2x)}}}This is where I got stuck. {{{(Sin5x(1+cosx))/(sinx(1+cos5x)) = (sin3x+sin2x)/(sin3x-sin2x)}

Algebra ->  Trigonometry-basics -> SOLUTION: please could you verify this? {{{(tan(5x/2))/(tan(x/2)) = (sin3x+sin2x)/(sin3x-sin2x)}}}This is where I got stuck. {{{(Sin5x(1+cosx))/(sinx(1+cos5x)) = (sin3x+sin2x)/(sin3x-sin2x)}      Log On


   

Question 1099317: please could you verify this? %28tan%285x%2F2%29%29%2F%28tan%28x%2F2%29%29+=+%28sin3x%2Bsin2x%29%2F%28sin3x-sin2x%29This is where I got stuck.
Found 2 solutions by Edwin McCravy, AnlytcPhil:
Answer by Edwin McCravy(20062) About Me  (Show Source):
You can put this solution on YOUR website!
To prove:

%28tan%285x%2F2%29%29%2F%28tan%28x%2F2%29%29%22%22=%22%22%28sin%283x%29%2Bsin%282x%29%29%2F%28sin%283x%29-sin%282x%29%29

Work with left side:

tan%285x%2F2%29%22%F7%22tan%28x%2F2%29

Change to sines and cosines:

%28sin%285x%2F2%29%29%2F%28cos%285x%2F2%29%29%22%F7%22%28sin%28x%2F2%29%29%2F%28cos%28x%2F2%29%29

Invert and multiply

%28sin%285x%2F2%29%29%2F%28cos%285x%2F2%29%29%22%22%2A%22%22%28cos%28x%2F2%29%29%2F%28sin%28x%2F2%29%29

%28sin%285x%2F2%29cos%28x%2F2%29%29%2F%28cos%285x%2F2%29sin%28x%2F2%29%29

%28sin%285x%2F2%29cos%28x%2F2%29%5E%22%22%29%22%F7%22%28cos%285x%2F2%29sin%28x%2F2%29%5E%22%22%29

Use a 'product to sum' formula, which is:

         sin%28A%29cos%28B%29%22%22=%22%22expr%281%2F2%29%28sin%28A%2BB%29%5E%22%22%2Bsin%28A-B%29%29
         [That's easy to prove using the formulas for sin(AħB)]

expr%281%2F2%29%28sin%285x%2F2%2Bx%2F2%29%5E%22%22%2Bsin%285x%2F2-x%2F2%29%29%22%F7%22expr%281%2F2%29%28sin%28x%2F2%2B5x%2F2%29%5E%22%22%2Bsin%28x%2F2-5x%2F2%29%29

expr%281%2F2%29%28sin%286x%2F2%29%5E%22%22%2Bsin%284x%2F2%29%29%22%F7%22expr%281%2F2%29%28sin%286x%2F2%29%5E%22%22%2Bsin%28-4x%2F2%29%29

expr%281%2F2%29%28sin%283x%29%5E%22%22%2Bsin%282x%29%29%22%F7%22expr%281%2F2%29%28sin%283x%29%5E%22%22%2Bsin%28-2x%29%29

Use the "odd-even" identity sin(-A) = -sin(A)

expr%281%2F2%29%28sin%283x%29%5E%22%22%2Bsin%282x%29%29%22%F7%22expr%281%2F2%29%28sin%283x%29%5E%22%22-sin%282x%29%29





%28sin%283x%29%5E%22%22%2Bsin%282x%29%29%2F%28sin%283x%29%5E%22%22-sin%282x%29%29

Edwin
AKA AnlytcPhil

Answer by AnlytcPhil(1807) About Me  (Show Source):
You can put this solution on YOUR website!
I tried it using the identity that you chose, but it became
more and more complicated, so I tried the "product to sum"
formula above, and, as you see, it was fairly straight forward.  
I could also have used the "sum to product" formula working 
with the right side.  The formulas you need for such problems are:

Sum or difference to product:

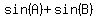
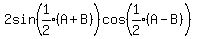
sin%28A%29%2Bsin%28B%29%22%22=%22%222sin%28expr%281%2F2%29%28A%2BB%29%29cos%28expr%281%2F2%29%28A-B%29%29

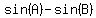
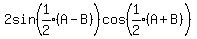
sin%28A%29-sin%28B%29%22%22=%22%222sin%28expr%281%2F2%29%28A-B%29%29cos%28expr%281%2F2%29%28A%2BB%29%29

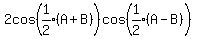
cos%28A%29%2Bcos%28B%29%22%22=%22%222cos%28expr%281%2F2%29%28A%2BB%29%29cos%28expr%281%2F2%29%28A-B%29%29

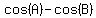
cos%28A%29-cos%28B%29%22%22=%22%22-2sin%28expr%281%2F2%29%28A%2BB%29%29sin%28expr%281%2F2%29%28A-B%29%29

Product to sum or difference

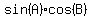
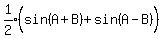
sin%28A%29cos%28B%29%22%22=%22%22expr%281%2F2%29%28sin%28A%2BB%29%2Bsin%28A-B%29%5E%22%22%29

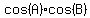
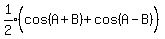
cos%28A%29cos%28B%29%22%22=%22%22expr%281%2F2%29%28cos%28A%2BB%29%2Bcos%28A-B%29%5E%22%22%29

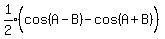sin%28A%29sin%28B%29%22%22=%22%22expr%281%2F2%29%28cos%28A-B%29-cos%28A%2BB%29%5E%22%22%29
 
All those are easily proved using formulas for sin(AħB) and cos(AħB)

Edwin
(AKA AnlytcPhil)