Question 1099301: Find the values of the trigonometric functions of the angle (in standard position) whose terminal side passes through the given point. (square root of 6, negative square root of 2)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Below, shown with the unit circle, is one such angle 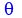 , ,
with the point 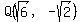 on its terminal side. on its terminal side.
Of course, there are infinitely many coterminal angles
with a terminal side going through Q:
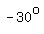 , , 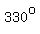 , , 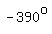 , , 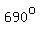 , etc. , etc.
They all have the same values for their trigonometric functions.
The negative angle 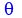 shown is the shown is the 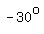 one. one.
It is in standard position,
and its trigonometric functions are derived from the coordinates of point P,
the point where the terminal side intersects the unit circle.

The absolute values of the trigonometric functions of 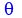
can be calculated as trigonometric ratios from triangle OBQ.
If you do it that way, keep in mind that being in quadrant IV,
sine, tangent, and cosecant should be given a negative sign.
The hypotenuse of The hypotenuse of OBQ is  . .
The legs of OBQ are
adjacent leg =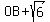 , and , and
opposite leg = . .
Otherwise, you could use the unit circle definition of trigonometric functions, and calculate them as the coordinates of point P.
The two blue right triangles OAP and OBQ are similar,
Triangle OAP is a scale-down version of OBQ,
all lengths made smaller by dividing by 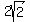 . .
(In equations  . .
So, the coordinates of P are
 , ,
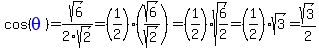




|
|
|