|
Question 1099296: I have this problem (the two equations should be in brackets with each other because they can be used to solve for each other):  and and  . I got two answers (0,2) and (6/5,8/5). Only the later answer solved completely. Does that mean it is the only real answer, or does this mean I got both answers wrong? Thanks for helping! . I got two answers (0,2) and (6/5,8/5). Only the later answer solved completely. Does that mean it is the only real answer, or does this mean I got both answers wrong? Thanks for helping!
Found 3 solutions by josgarithmetic, MathTherapy, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! A circle and a line;
They can intersect in NO MORE THAN two points.
Does that help you? It should and should easily make sense.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have this problem (the two equations should be in brackets with each other because they can be used to solve for each other):  and and  . I got two answers (0,2) and (6/5,8/5). Only the later answer solved completely. Does that mean it is the only real answer, or does this mean I got both answers wrong? Thanks for helping! . I got two answers (0,2) and (6/5,8/5). Only the later answer solved completely. Does that mean it is the only real answer, or does this mean I got both answers wrong? Thanks for helping!
One of the coordinates of the 1st coordinate point is WRONG. The 2nd is fine.
Look over your solution for the 1st coordinate point.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First of all, by substituting your "solutions" directly into the given equations ("the "CHECKING" step)
you can see that (0,2) IS NOT THE SOLUTION, while (6/5,8/5) IS.
Let solve this system together:
 = 4, (1)
3x - y = 2. (2)
From (2), express y = 3x-2. Next, substitute it into equation (1), replacing "y". You will get = 4, (1)
3x - y = 2. (2)
From (2), express y = 3x-2. Next, substitute it into equation (1), replacing "y". You will get
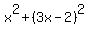 = 4.
Simplify it step by step: = 4.
Simplify it step by step:
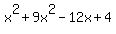 = 4 ====> = 4 ====> 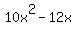 = 0 ====> (factoring left side) ====>
2x*(5x-6) = 0.
The solutions for x are 0 and x= = 0 ====> (factoring left side) ====>
2x*(5x-6) = 0.
The solutions for x are 0 and x= 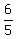 .
a) If x= 0, then from (2) y = 3x-2 = 3*0-2 = -2.
So, the pair (x,y) = (0,-2) is one solution.
b) If x= .
a) If x= 0, then from (2) y = 3x-2 = 3*0-2 = -2.
So, the pair (x,y) = (0,-2) is one solution.
b) If x= 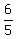 , then y = 3x-2 = , then y = 3x-2 = 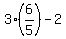 = = 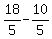 = = 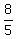 .
So, the pair (x,y) = (6/5,8/5) is the other solution.
Answer. The solutions are (0,-2) and (6/5,8/5). .
So, the pair (x,y) = (6/5,8/5) is the other solution.
Answer. The solutions are (0,-2) and (6/5,8/5).
You can CHECK that these pairs satisfy both original equations.
---------------
To see more solved problems for systems of equations of this type, look into the lessons
- Solving the system of algebraic equations of degree 2 and degree 1,
- Solving the system of algebraic equations of degree 2,
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of equations that are not linear".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
| |