Question 1099289: Find f(x) given that
f'(x) = x^3 − 2√x, f(1) = 4
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The derivative of a sum of functions is the sum of the derivatives,
so the same applies to antiderivatives,
So to find a function with 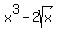 for a derivative, for a derivative,
we need to find what function has for derivative  , ,
and what function has for derivative  . .
We also know that if we find a function with 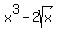 for a derivative, for a derivative,
adding any constant  , we get another function with the same derivative. , we get another function with the same derivative.
We will use  to figure out what constant to add. to figure out what constant to add.
We know about derivatives of polynomials.
For any exponent  (integer or not, as long as (integer or not, as long as 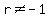 ), ),
if  , ,  , ,
and that lets us figure out the antiderivative of any  , ,
except  . .
So, the antiderivative of  is is 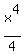 ; ;
and the antiderivative of  is is  . .
So, we can see that 
for some constant  . .
Then,  . .
If  , ,


 , ,
and 
|
|
|