SOLUTION: FOR A TREE PLANTATION,IT WAS DECIDED TO DIVIDE THE SAPLING IN TO EQUAL GROUPS OF 24 OR 30 OR 32 SUCH THAT NO SAPLING ARE LEFT.WHAT IS THE MINIMUM NUMBER OF SAPLINGS WHICH MAKES THI

Actually, the problem asks about Least Common Multiple (LCM) of the numbers 24, 30 and 32.


24 = ,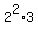

30 = ,

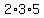32 = .


Thus LCM must include factors  , 3 and 5.


Therefore,  LCM(24,30,32) = 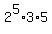 = 480.


Answer.  

    WHAT IS THE MINIMUM NUMBER OF SAPLINGS WHICH MAKES THIS POSSIBLE?  480.


    HOW MANY GROUPS CAN BE MADE,IF EACH GROUP HAS 24 SAPLINGS? 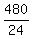         = 20 group.