Question 1099143: The number of people in a community who hear a particular rumor is governed by the
logistic model
R(t) =
L 1 + Me−κt where R(t) represents the number of people who have heard the rumor t days after the
rumor initially was told by one person to another person. The constants L, M and κ
are to be determined from observations of the spreading rumor.
The following observations of the rumor “The cake is a lie” spreading across a uni
versity campus are made • Initially one student tells another student the rumor, that is, only 2 students have heard the rumor. • The rumor spreads to 10 students after 1 day. • After a number of days of observations it is predicted that eventually, that is, after a very long time, 200 students on campus will have heard the rumor.
Given the three pieces of information provided from the observations of the rumor, find
the exact values of the constants L, M and κ. Write the equation describing how many
people have heard the rumor at time t days after the rumor starts
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The logistic function is

The numerator "L" is the limiting value of the function, as t goes to infinity. This is because as t gets very large, the expression 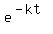 goes to 0, making the function value L/1 = L. goes to 0, making the function value L/1 = L.
So in your problem, L is 200, and the function is

The function value at t=0 is the starting value of the function. The function evaluated at t=0 is 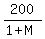 , because when t=0 , because when t=0  . .
In your problem, where the initial number of people who have heard the rumor is 1, we have  which means M is 199. which means M is 199.
So the function in this problem is

To find the value of k to finish the problem, we use the given information that 10 students have heard the rumor after 1 day. That is, R(1) = 10.




Now in the denominator of the logistic function, notice that 
Since we have found that the value of 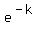 is is 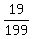 ; we can now write the completed function for this problem as ; we can now write the completed function for this problem as

With the logistic function in this form, it is easy to see that the given three data points are satisfied:
(1) 
(2) 
(3) For t "large", 
Now I note that the way you have asked the question, we are supposed to find the values of L, M, and k. Finding the values of L and M was easy.
But we didn't find the value of k in the work above. However, that is easy:



We could write the logistic function using 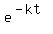 ; but it would look ugly: ; but it would look ugly:

|
|
|