Question 1099029: Let there are four numbers, the first three are geometric progression and the last three numbers are arithmetic progression. If the sum of the means is 24 and the sum of the extremes is 32 find the numbers?
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Let the first term be x, and let the common ratio of the geometric sequence be r. Then the first three terms of the sequence are
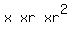
The last three of the four terms form an arithmetic sequence. The difference between the second and third terms is 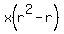 ; so the fourth term is the third term, plus that difference: 
So now the means are  and 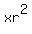 , and the extremes are  and 
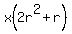
The sum of the means is 24, and the sum of the extremes is 32:
We can divide these two equations one by the other to eliminate x, giving us an equation we can solve for a:
Somewhat surprisingly -- to me, at least -- it appears we have two potential solutions to the problem. Let's see if they both work....
(1) If r = 3...
The sequence is x, 3x, 9x, 15x.
x+15x = 32; 16x = 32; x=2. The sequence is 2, 6, 18, 30. Yes; that one works.
(2) If r = 1/2...
The sequence is x, x/2, x/4, 0.
x+0 = 32; x = 32. The sequence is 32, 16, 8, 0. Yes, that one works also.
There are two sequences that satisfy the given conditions:
2, 6, 18, 30 and 32, 16, 8, 0.
|
|
|
