Question 1098878: Consider the function f(x) = xe^x
.
(a) State the domain of f.
(b) Find the vertical asymptotes and horizontal asymptotes of the curve y(x) = f(x), if exist.
(c) Find the stationary points of the curve y(x) = f(x) and use the second derivative test to determine their nature.
(d) Find the points of inflection.
(e) Determine the x− and y− intercepts.
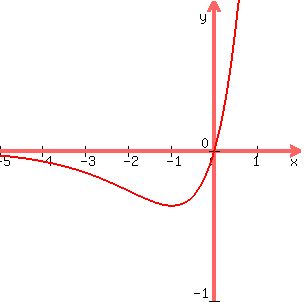
(f) Sketch the curve using known information.
(g) State the range of f.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x)=x*e^x
A)domain is all x

B)Horizontal asymptote is 0-, as x approaches -oo. No vertical asymptotes.
C) derivative is x*e^x+e^x. Set it equal to 0 and e^x(x+1)=0 and x=-1, stationary point at (-1, -e^(-1)) or (-1, -1/e).
D) Inflection point is derivative of e^x*(x+1). This is e^x+(x+1)^e^x=e^x(x+2)
Set that equal to 0, and x=-2, so infection point is (-2, -2/e^2)
E) when y=0 x=0, so (0, 0) is y intercept and x intercept.
G. Range is (-1/e, +oo)
|
|
|