Question 1098822: Hi
there were 900 sweets in boxes a b c.18 sweets were transfered from a to b.5 sweets were transferred from b to c.1/3 of the sweets in c were then transferred to a.there were an equal number of sweets in all 3 boxes. How many sweets were in each box at first.
thanks
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52899)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The condition says that after all exchanges there were an equal number of sweets in all 3 boxes.
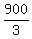 = 300, which means that finally there were 300 sweets in each box.
Further, the condition says
a - 18 + = 300, which means that finally there were 300 sweets in each box.
Further, the condition says
a - 18 + 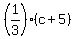 = 300, (1)
b + 18 - 5 = 300, (2)
(c+5) - = 300, (1)
b + 18 - 5 = 300, (2)
(c+5) - 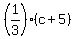 = 300. (3)
From (3), = 300. (3)
From (3), 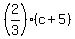 = 300 ====> c+5 = = 300 ====> c+5 =  = = 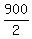 = 450 ====> c = 450-5 = 445.
From (2), b = 300 + 5 - 18 = 287.
From (1), a = 300 - = 450 ====> c = 450-5 = 445.
From (2), b = 300 + 5 - 18 = 287.
From (1), a = 300 -  + 18 = 300 - 150 + 18 = 168.
Answer. Originally, there were 168 sweets in A, 287 sweets in B and 445 sweets in C. + 18 = 300 - 150 + 18 = 168.
Answer. Originally, there were 168 sweets in A, 287 sweets in B and 445 sweets in C.
Solved.
There is NO NEED to solve system in 3 equations in 3 unknowns.
This problem is for young students (5 - 6 grades) who have no any notion on systems of equations.
The solution and the approach by @josgarithmetic go entirely and totally out of the target.
For your safety, simply ignore his writing.
|
|
|