SOLUTION: x^2+xy+yz+zx=30 y^2+xy+yz+zx=15 z^2+xy+yz+zx=18 find x^2+y^2+z^2

Step 1.  Factor left side of each equation. You will get

    x^2+xy+yz+zx = 30    is the same as    (x+y)*(x+z) = 30    (1)
    y^2+xy+yz+zx = 15    is the same as    (x+y)*(y+z) = 15    (2)
    z^2+xy+yz+zx = 18    is the same as    (x+z)*(y+z) = 18    (3)



Step 2.  Multiply equations (1), (2) and (3)  (left sides and right sides). You will get


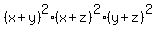     = 30*15*18 = (15*2)*15*(2*3^2) =  =  = .

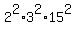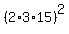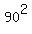    Take the square root of both sides.  You will get  (x+y)*(x+z)*(y+z) = +/- 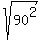,   or

    (x+y)*(x+z)*(y+z) = +/- 90.    (4)



Step 3.  First, let us consider the case

    (x+y)*(x+z)*(y+z) = 90.        (5)


    Divide eq(5) by eq(1) (both sides).  You will get    y + z = 3.       (6)    (3 = 90/30)

    Divide eq(5) by eq(2) (both sides).  You will get    x + z = 6.       (7)    (6 = 90/15)

    Divide eq(5) by eq(3) (both sides).  You will get    x + y = 5.       (8)    (5 = 90/18)



Step 4.  To solve the system (6), (7), (8), add all three equation (6), (7) and (8) (both sides). You will get

    
    2x + 2y + 2z = 3 + 6 + 5 = 14.  It implies           x + y + z = 7.   (9)


    Now   subtract eq(6) from eq(9)  (both sides).   You will get  x = 7-3 = 4.

    Next, subtract eq(7) from eq(9)  (both sides).   You will get  y = 7-6 = 1.

    Next, subtract eq(7) from eq(9)  (both sides).   You will get  z = 7-5 = 2.


    So, (x,y,z) = (4,1,2) is the solution in this case.


Step 5.  Now let us consider the case

    (x+y)*(x+z)*(y+z) = -90.        


    Doing by the same way, you will obtain the solution  (x,y,z) = (-4,-1,-2)  in this case.


Step 6.  Check.  It is enough to check the positive solution only.

     
    4^2 + 4*1 + 4*2 + 1*2 = 30.     ! Correct !
    1^2 + 4*1 + 4*2 + 1*2 = 15.     ! Correct !
    2^2 + 4*1 + 4*2 + 1*2 = 18.     ! Correct !


Answer.  The given system has two and only two solutions  (x,y,z) = (4,1,2)  and  (x,y,z) = (-4,-1,-2).

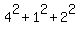         Therefore,   =  = 21.