SOLUTION: Abby drove from town A to B in 3 hours. Billy left town A at the same time, but drove 5km/h more slowly, and arrived at town B 20 minutes later than Abby. What is the distance betw

Let "r" be the Andy's rate, in kilometers per hour.

Then the Billy's rate was  (r-5) km/h.


Abby covered the distance  r*3  in three hours.

Billy covered the distance (r-5)*(3 + 1/3)   (notice that 1/3 = 1/3 of an hour = 20 minutes).


The distance is the same, which gives you an equation 

3r = (10/3)*(r-5).


Simplify and solve for r. First step is to multiply both sides by 3 and open parentheses:

9r = 10r - 50  ====>   50 = 10r - 9r  ====>  r = 50.


Thus Andy's rate was 50 km/h.


Hence, the distance between the towns was 3*50 = 150 km.

Let D be the distance between the towns.


Andy's rate was   kilometers per hour.

Billy's rate was 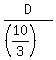  kilometers per hour.    (Notice that  =  hours).


The difference of the rates was 5 km/h, according to the condition.

It gives you an equation

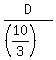 -  = 5,   or, which is the same

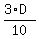 -  = 5.

Multiply both sides by 30. You will get

10D - 9D = 5*30  ====>  D = 150.


You got the same answer:  The distance is 150 kilometers.