Question 1098319: Determine the zeros, the degree, and the leading coefficient to graph this function.
f(x) = (x2+2x)(x-3)
Found 3 solutions by greenestamps, ankor@dixie-net.com, KMST:
Answer by greenestamps(13209)   (Show Source):
You can put this solution on YOUR website!
Factor the expression in the first set of parentheses to get
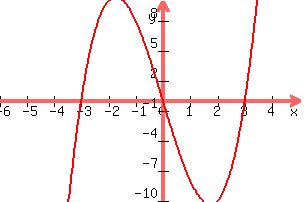
With the function written this way, it is clear that the function is of degree 3 with leading coefficient 1 (leading term x^3), and with zeros at 0, -2, and 3.
Except for the exact y values, the degree, the leading coefficient, and the zeros together give a good picture of the general behavior of the graph.
Answer by ankor@dixie-net.com(22740)  (Show Source):
You can put this solution on YOUR website! Determine the zeros, the degree, and the leading coefficient to graph this function.
f(x) = (x^2 + 2x)(x - 3)
Find the 0's
x^2 + 3x = 0
Factor out x
x(x + 3) = 0
x = 0
and
x = -3
@nd factor
x = 3
The zeros -3, 0, 3
The degree is 3 and leading coefficient is 1 but you can confirm that:
FOIL
(x^2+3x)*(x-3) = x^3 - 3x^2 + 3x^2 - 9x = x^3 - 9x
:
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! Usually, we write exponents following a ^ symbol.
Write  as x^2 ,  as x^3 and  as sqrt(2),
and people will know what you mean.
You probably mean
Factorinng further the  factor,
you can re-write the fucntion as
When one of those three factors is zero,  ,
so the zeros of the function are
 ,
 <-->  , and
 <-->  .
Doing the indicated multiplication,
can be re-written as  ,
and "collecting like terms, we simplify it to
The leading coefficient is the number part of the term of highest degree.
That is the implied/invisible  in front of .
The degree is the greatest exponent: the  in .
|
|
|
