Question 1098023: A tank of water is contaminated with 58 pounds of salt. In order to bring the salt concentration down to a level consistent with EPA standards, clean water is being piped into the tank, and the well-mixed overflow is being collected for removal to a toxic-waste site. The result is that at the end of each hour there is 24% less salt in the tank than at the beginning of the hour. Let S = S(t) denote the number of pounds of salt in the tank t hours after the flushing process begins.
(a) Explain why S is an exponential function.
The amount of salt is being decreased by .24 PERCENT each hour, so the decay is at a CONSTANT PORPOTIONAL rate.
Find its hourly decay factor.
0.76
(b) Give a formula for S.
S = 58·0.76t
(c) Make the graph of S that shows the flushing process during the first 15 hours.
got this one correct
Describe in words how the salt removal process progresses.
LARGE amounts of salt are removed early in the process, and, as time passes, the rate of removal DECREASES.
(d) In order to meet EPA standards, there can be no more than 3 pounds of salt in the tank. How long must the process continue before EPA standards are met? (Round your answer to two decimal places.)
10.79hr
(e) Suppose this cleanup procedure costs $8000 per hour to operate. How much does it cost to reduce the amount of salt from 58 pounds to 3 pounds? (Round your answer to the nearest dollar.)
$ 86320
How much does it cost to reduce the amount of salt from 3 pounds to 0.1 pound? (Round your answer to the nearest whole dollar.)
$ HELP ME CAN NOT GET
already had the hours that it would take to get from 58 lbs to 3 lbs, then did log formula and found how long for 58 lbs to 0.01lbs and then took that value and subtracted and them rounded to the hundredths place and then multiplied by $8,000. but that is wrong so help
Answer by ikleyn(52754)   (Show Source):
You can put this solution on YOUR website! .
A tank of water is contaminated with 58 pounds of salt. In order to bring the salt concentration down to a level consistent
with EPA standards, clean water is being piped into the tank, and the well-mixed overflow is being collected for removal
to a toxic-waste site. The result is that at the end of each hour there is 24% less salt in the tank than at the beginning
of the hour. Let S = S(t) denote the number of pounds of salt in the tank t hours after the flushing process begins.
(a) Explain why S is an exponential function.
The amount of salt is being decreased by  24 PERCENT each hour, so the decay is at a CONSTANT  EXPONENTIAL rate.
Find its hourly decay factor.
0.76
(b) Give a formula for S.
S = 58·0.76t <<<---=== WRONG formula. The correct formula is S(t) = 
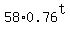(c) Make the graph of S that shows the flushing process during the first 15 hours.
got this one correct
Describe in words how the salt removal process progresses.
LARGE amounts of salt are removed early in the process, and, as time passes, the rate of removal DECREASES.
(d) In order to meet EPA standards, there can be no more than 3 pounds of salt in the tank. How long must the process continue
before EPA standards are met? (Round your answer to two decimal places.)
10.79hr
(e) Suppose this cleanup procedure costs $8000 per hour to operate. How much does it cost to reduce the amount of salt
from 58 pounds to 3 pounds? (Round your answer to the nearest dollar.)
$ 86320
How much does it cost to reduce the amount of salt from 3 pounds to 0.1 pound? (Round your answer to the nearest whole dollar.)
$ HELP ME CAN NOT GET
already had the hours that it would take to get from 58 lbs to 3 lbs, then did log formula and found how long for 58 lbs to 0.01 lbs
and then took that value and subtracted and them rounded to the hundredths place and then multiplied by $8,000. but that is wrong so help
<<<---=== Your steps, as you described them, were/are correct.
My only notice is that they ask about 0.1 lbs,
while you made your calculations for 0.01 lbs
(according to your text)
|
|
|
