Question 1097414: The stopping distance d of a car after the brakes are applied varies directly as the square of the speed r. If a car traveling 50 mph can stop in 110 ft, how many feet will it take the same car to stop when it is traveling 100 mph? It will take how many feet? Please give exact answer!!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! When a variable (like braking distance, d, in feet)
varies directly with some other variable (like the square of the speed, with r=speed measured in mph),
as one variable changes by a factor, so does the other.
As the speed doubles, from 50 mph to 110 mph,
the square of the speed quadruples.
It changes from  to  ,
but we do not need to calculate to know
that when one number doubles its square quadruples.
The square of the speed quadrupled,
and so does the breaking distance,
from  to  .
Easy mental math.
If you were asked to write it as a function,
you would define  as a positive constant,
say that
 ,
and substituting 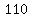 for the distance and  for the speed,
you would find :
 -->  -->  -->  .
Then, the function,would be
 .
Then, you could use that function,
substituting  for  ,
to calculate the answer as
 .
That would require a lot more writing and calculating.
|
|
|
