Question 1097176: four children earn money for a charity, dauda earns #y, obi earns half as much as dauda, chidi earns three times as much as Obi and Wale earns #250 less than all the other three. together they earn more than #4300, find the least value of y?
Found 3 solutions by Fombitz, josmiceli, MathTherapy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
four children earn money for a charity, dauda earns #y, obi earns half as much as dauda, chidi earns three times as much as Obi and Wale earns #250 less than all the other three. together they earn more than #4300, find the least value of y?
When possible, STAY AWAY from fractions. However, it's better to use them in this case.
As suggested, Dauda earns y
Therefore, Obi earns 
Chidi earns: 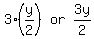
Wale earns 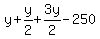
We then get: 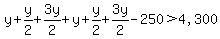

y + 2y + y + 2y - 250 > 4,300
6y > 4,550

The least value of y will then be: 
|
|
|