Question 1097086: A five figure number is formed by the digit 0,1,2,3,4 without repetition. Find the probability that the number formed is divisible by 4.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the first digit can't be 0, the number of different 5-digit numbers we can make with these digits is 4*4*3*2*1 = 96.
With these digits, if the number is to be divisible by 4, the possibilities for the sequence of final two digits are
04, 12, 24, or 32
We look at separate cases for each of the possible first digits (1, 2, 3, or 4)
For each case, we determine which of the four possible sequences of final two digits are possible.
For each of the cases we find with a given first digit and allowable last two digits, there are two different ways to place the remaining two digits in positions 2 and 3.
first digit 1: 3 of the 4 sequences of final two digits are possible, so 3*2=6 solutions
first digit 2: only 1 of the 4 sequences of final two digits is possible, so 1*2 = 2 solutions.
first digit 3: again 3 of the 4 sequences of final two digits are possible, so 3*2=6 solutions
first digit 4: 2 of the 4 sequences of final two digits are possible, so 2*2=4 solutions
The total number of 5-digit numbers using these digits that are divisible by 4 is 6+2+6+4 = 18
The probability that a 5-digit number formed using these digits is divisible by 4 is 18/96 = 3/16.
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
0) Since the first digit can't be 0, the number of different 5-digit numbers we can make with these digits is 4*4*3*2*1 = 96.
In order for the number is divisible by 4, the last two digits must be
04, 12, 24, 32, 20 and/or 40.
1) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 04, then in the 123-positions we have all permutations of the three digits
1, 2 and 3, which gives us 3! = 6 numbers.
2) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 12, then in the 123-positions we have permutations of the three digits
0, 3 and 4, with prohibited 0 in the first position, which gives us 2*2*1 = 4 numbers.
3) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 24, then in the 123-positions we have permutations of the three digits
0, 1 and 3, with prohibited 0 in the first position, which gives us again 2*2*1 = 4 numbers.
4) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 32, then in the 123-positions we have permutations of the three digits
0, 1 and 4, with prohibited 0 in the first position, which gives us again 2*2*1 = 4 numbers.
5) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 20, then in the 123-positions we have all permutations of the three digits
1, 3 and 4, which gives us 3! = 6 numbers.
6) If the last two digits (in the 4-th and 5-th positions, counting from the left)
are 40, then in the 123-positions we have all permutations of the three digits
1, 2 and 3, which gives us 3! = 6 numbers.
7) Thus we have 96 allowed 5-digit numbers in all; of them exactly 6 + 4 + 4 + 4 + 6 + 6 = 30 are divisible by 4.
Therefore, the probability under the question is 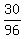 = =  . .
|
|
|