Question 1097012: Ben was in charge of ordering 16 pizzas for the office party. He ordered three types of pizza: Cheese, Pepperoni, and Supreme. The cheese pizzas cost $8 each, the pepperoni pizzas cost $10 each, and the supreme pizzas cost $12 each. He spent exactly twice as much on the pepperoni pizzas as he did on the cheese pizzas. If Ben spent a total of $156 on pizza, how many pizzas of each type did he buy?
Found 4 solutions by Boreal, jorel1380, stanbon, MathTherapy:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! C=x--$8
P=y--$10
S=16-(x+y)--$12. We know that S pizzas are everything up to 16 that hasn't been accounted for.
8x+10y+12(16-(x+y)=$156
We know that 10y=16x
Therefore, we have
8x+16x+192-12(x+1.6x)=156
24x+192-31.2x=156
-7.2x=-36
x=5
cost of C pizzas is $8*5=$40
Therefore P=$80, and that would be 8 P pizzas.
That leaves 3 S pizzas, and those would be $36
The cost adds to $156; the number to 16.
Keep it in two variables, x and y. The Supremes are everything left or 16-(x+y).
Answer by jorel1380(3719)  (Show Source):
You can put this solution on YOUR website! Let c, p, and s be the number of cheese, pepperoni, and supreme pizzas ordered, respectively. Then:
c+p+s=16, and
8c+10p+12s=156
Also:
10p/2=8c
10p=16c
p=16c/10
So:
c+16c/10+s=16
26c+10s=160
24c+12s=156
Solve for c and s (then you can calculate p)
☺☺☺☺
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! Ben was in charge of ordering 16 pizzas for the office party. He ordered three types of pizza: Cheese, Pepperoni, and Supreme. The cheese pizzas cost $8 each, the pepperoni pizzas cost $10 each, and the supreme pizzas cost $12 each. He spent exactly twice as much on the pepperoni pizzas as he did on the cheese pizzas. If Ben spent a total of $156 on pizza, how many pizzas of each type did he buy?
------
Quantity Equation:: c + p + s = 16
Value Equation:: 8c + 10p + 12s = 156
Value:: 10p = 2(8c)
--------------------------------
Rearrange::
c + p + s = 16
8c+10p+12s = 156
16c-10p+0s = 0
--------------------
Use any method you know to solve the system
to get
c = 5
p = 8
s = 3
------
Cheers,
Stan H.
--------------
Answer by MathTherapy(10549)  (Show Source):
You can put this solution on YOUR website!
Ben was in charge of ordering 16 pizzas for the office party. He ordered three types of pizza: Cheese, Pepperoni, and Supreme. The cheese pizzas cost $8 each, the pepperoni pizzas cost $10 each, and the supreme pizzas cost $12 each. He spent exactly twice as much on the pepperoni pizzas as he did on the cheese pizzas. If Ben spent a total of $156 on pizza, how many pizzas of each type did he buy?
Let number of cheese, pepperoni, and supreme, be C, P, and S, respectively
Then we get: C + P + S = 16 -------- eq (i)
8C + 10P + 12S = 156 -------- eq (ii)
10P = 2(8C)___10P = 16C______ -------- eq (iii)
8C + 16C + 12S = 156_____24C + 12S = 156_____2C + S = 13 ---- Replacing 10P in eq (ii) with 16C, and reducing it ------- eq (iv)
 -------- Replacing 
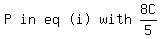
5C + 8C + 5S = 80______13C + 5S = 80 ------ Multiplying by LCD, 5 ------- eq (v)
- 10C - 5S = - 65 ------- Multiplying eq (iv) by - 5 -------- eq (vi)
3C = 15 ------ Adding eqs (vi) & (v)
Number of cheese pizzas purchased, or 
2(5) + S = 13 ------- Substituting 5 for C in eq (iv)
10 + S = 13
Number of supreme pizzas purchased, or 
Number of pepperoni pizzas purchased, or  ------- Substituting 5 for C in eq (iii)
|
|
|
