Question 1096884: A car dealership has 7 red, 14 silver, and 4 black cars on the lot. Ten cars are randomly chosen to be displayed in front of the dealership.
a) Find the probability that 4 cars are red and that the rest are silver.
b) Find the probability that 6 cars are red and 4 cars are black.
c) Find the probability that exactly 7 cars are red.
HELP. Please answer with Full Details.
Thank you
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I will assume since you are working a problem like this that you are familiar with "n choose r", which I will represent with C(n,r). That number is the number of ways of choosing r of n identical objects.
Overall, you are choosing 10 of the total 25 cars for the display, so the total number of possible choices (the denominator of your probability fraction) is C(25,10).
For case (a), you need to choose 7 of the 7 red cars, AND 3 of the 14 silver cars, AND 0 of the 4 black cars. As always when calculating probabilities, those "AND"s mean you are going to multiply the individual probabilities. So for case (a), the numerator is [C(7,7)*C(14,3)*C(4,0)]
Answer for part (a): 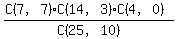
By similar analysis, the answer for part (b) is 
For part (c) we need to do a bit more work. We know all 7 red cars must be chosen (C(7,7)); but we could have either 3 silver and 0 black, OR 2 silver and 1 black, OR 1 silver and 2 black, OR 0 silver and 3 black. And again, as always in probability those "OR"s mean we will be adding probabilities.
So the numerator for case (c) is C(7,7) multiplied by the SUM of C(14,3)*C(4,0), C(14,2)*C(4,1), C(14,1)*C(4,2), and C(14,0)*C(4,3).
Answer for part (c):

|
|
|