SOLUTION: Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. 4, -14, and 5 + 8i

Given zeros:

4, -14, and 5 + 8i

Let p(x) be the polynomial. 
Since 5+8i is a zero of p(x), and the polynomial has real coefficients
then so is its conjugate 5-8i, so four of the zeros of p(x) are

4, -14, 5+8i and 5-8i, so the solutions to the equation p(x)=0 are: 

, , , 

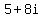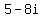Get 0 on the right of those four equations:

, , , 

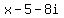
Multiply the left and right sides





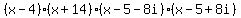
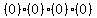
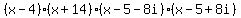
If we want p(x) to have leading coefficient 1, 
and have only those four zeros and no others, then
it will have leading coefficient x4 and
be of degree 4.


 
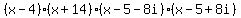Now you'll have to multiply that out all by yourself,
which is a big job.  But when you finish you'll get:



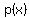
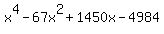Edwin