SOLUTION: By how much does the arc intercepted by a central angle of 38 degrees exceed the chord intercepted by the same angle on a circle of radius 43 ft.? Please help me :(

Algebra ->  Trigonometry-basics -> SOLUTION: By how much does the arc intercepted by a central angle of 38 degrees exceed the chord intercepted by the same angle on a circle of radius 43 ft.? Please help me :(      Log On


   

Question 1096676: By how much does the arc intercepted by a central angle of 38 degrees exceed the chord intercepted by the same angle on a circle of radius 43 ft.?

Please help me :(
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
NOTE:
I assume this is math homework,
and not physics homework.
I also assume that the answer is expected to be a length in feet,
because if the expected answer was 1.9%,
There would be no need to know the radius.
In that case, you would compare the length of
a 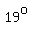19%5Eo arc on a unit circle with
(the measure of the arc in radians)
to the sine of 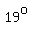19%5Eo ,
to find that
%2819%2Api%2F180%29%2Fsin%2819%5Eo%29=about1.0185657

A PICTURE AND THEN AN ANSWER IN 1,000 WORDS:


LENGTH OF THE ARC:
Using radians:
The angle measure 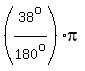38%5Eo is %2838%5Eo%2F180%5Eo%29%2Api in radians.
The length of an arc of that measure is
angle in radians times radius.
For a circle of 43ft radius, it is 19%2A43pi%2F90 .
Without radians:
The whole circumference is 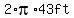2%2Api%2A43ft .
The arc is a fraction of that. It is 38%5Eo%2F360%5Eo=19%2F180 .
So, the arc length is %2819%2F180%29%2A2%2Api%2A43ft=19%2A43%2Api%2F90ft .
That is approximately 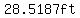28.5187ft .

LENGTH OF THE CHORD:
Connecting the ends of the chord to the center of the circle,
you form an isosceles triangle.
It has two legs measuring 43ft forming an angle measuring 38%5Eo .
It's base is the chord, whose length x we need to find
If Law of cosines was taught in class, you may be expected to use it.
.
So, chord=sqrt%282-2cod%2838%5Eo%29%29%2A%2843ft%29
That is approximately 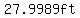27.9989ft .

Otherwise, you could split that triangle into two right triangles,
and use trigonometry to find the length of half the chord as
sin%2819%5Eo%29%2A%2843ft%29=approximately13.99943ft ,
so the length of the chord is twice that,
or approximately 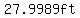27.9989ft .

By how much does the arc exceed the chord?
We calculate the difference as about 28.5187ft-27.9989ft=0.5198ft ,
So, I would answer highlight%280.52ft%29 .

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
By how much does the arc intercepted by a central angle of 38 degrees exceed the chord intercepted by the same angle on a circle of radius 43 ft.?

Please help me :(
Let central angle be O, radii AO and BO, and intercepted chord & intercepted arc, AB

∡A = 38o

Length of arc AB: 



∡A and ∡B = matrix%281%2C5%2C+%28180+-+38%29%2F2%2C+%22=%22%2C+142%2F2%2C+%22=%22%2C+71%5Eo%29 

Draw an altitude from vertex O to AB, and name it C

cos ∡A = matrix%281%2C3%2C+A%2FH%2C+%22=%22%2C+AC%2FAO%29

matrix%281%2C3%2C+cos+%2871%5Eo%29%2C+%22=%22%2C+AC%2F43%29

matrix%281%2C5%2C+AC%2C+%22=%22%2C+43%2C+%22%2A%22%2C+cos+%2871%5Eo%29%29 --------- Cross-multiplying

AC = 14

Since the altitude from vertex O, or OC BISECTS chord AB, AC = matrix%281%2C3%2C+%281%2F2%29%2C+of%2C+AB%29. Therefore, the INTERCEPTED CHORD or matrix%281%2C6%2C+AB%2C+%22=%22%2C+2%2814%29%2C+or%2C+28%2C+feet%29

Arc AB exceeds chord AB by .