|
Question 1096650: Last Tuesday Regal Cinemas sold a total of 8500 movie tickets. Proceeds totalled $64600. Tickets can be bought in one of the three ways. A matinee admission costs $5, student admission is $6 all day, regular admissions are $8.50. How many of each type were sold if twice as many student tickets were sold as matinee tickets?
Found 2 solutions by CubeyThePenguin, ikleyn:
Answer by CubeyThePenguin(3113)   (Show Source):
You can put this solution on YOUR website! r = number of regular tickets
s = number of student tickets
m = number of matinee tickets
r + s + m = 8500
8.5r + 6s + 5m = 64600
s = 2m
Plug the third equation (s = 2m) into the other equations.
r + 3m = 8500
8.5r + 17m = 64600
You can use any method (substitution, elimination, graphing) to solve for r and m. Plug those values back into the first equation and you are done.
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
Last Tuesday Regal Cinemas sold a total of 8500 movie tickets. Proceeds totalled $64600.
Tickets can be bought in one of the three ways. A matinee admission costs $5, student admission is $6 all day,
regular admissions are $8.50. How many of each type were sold if twice as many student tickets were sold as matinee tickets?
~~~~~~~~~~~~~~
It is a typical problem to be solved using only one single unknown.
Let x be the number of the matinee tickets.
Then the number of the student tickets is 2x,
and the number od the regular admission tickets is (8500-x-2x) = (8500-3x).
Now you write the total money equation (the revenue)
5x + 6*(2x) + 8.50*(8500-3x) = 64600 dollars.
Simplify and solve for x
5x + 12x - 8.50*3*x = 64600 - 8.50*8500
x = 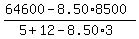 = 900.
ANSWER. 900 matinee tickets; 2*900 = 1800 student tickets and the rest, 8500-900-1800 = 5800, were the regular admission tickets.
CHECK. 900*5 + 1800*6 + 5800*8.50 = 64600 dollars, in total. ! Correct !
Solved.
---------------
From my post, learn how to solve such problems using one single unknown variable, only.
It is the major lesson to learn from my solution.
|
|
|
| |
