SOLUTION: A field in the shape of a right triangle has an area of 30 square meters. If one leg of the right triangle that forms the field is 4 meters longer than the other leg, what is t

Algebra ->  Pythagorean-theorem -> SOLUTION: A field in the shape of a right triangle has an area of 30 square meters. If one leg of the right triangle that forms the field is 4 meters longer than the other leg, what is t      Log On


   

Question 1096436: A field in the shape of a right triangle has an area of
30 square meters. If one leg of the right triangle that forms the field is
4 meters longer than the other leg, what is the length of the longer leg?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The area of a right triangle can be calculated as
area=leg%5B1%5D%2Aleg%5B2%5D%2F2 ,
Because if we call one leg the base of the triangle,
the other leg is the altitude.

In this case, leg lengths in meters are x and x%2B4 ,
so x%28x%2B4%29%2F2=30 ,
x%28x%2B4%29=30%2A2 ,
x%5E2%2B4x=60 ,
x%5E2%2B4x-60=0 , and
%28x-6%29%2A%28x%2B10%29=0 .
The solution is highlight%28x=6%29 from x-6=0 .
The other solution to the equation, x=-10 from x%2B10=0
is not a solution to the problem,
because x is the length of a triangle side in meters,
and it must be a positive number.
So, the length of the shorter leg is 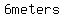6meters ,
and the length of the longer leg is 6meters%2B4+meters=highlight%2810meters%29 .