SOLUTION: for the ellipse x^2/a^2 + y^2/b^2=1 with foci at (-c,0) and (c,0), show that b^2 = a^2 – c^2

 
The definition of an ellipse is:
 
An ellipse is a curved line forming a closed loop, where the sum 
of the distances from two points (foci) to every point on the line 
is constant.
 
Therefore since (0,b), and (a,0) are points on the ellipse,

the sum of the distances indicated by the two red lines must be equal
to the constant, and also the sum of the two straight distances 
indicated by the two green curved lines must also equal the the same
constant. 
 

 

 





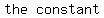
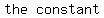
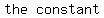
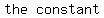Since a > c > 0, then, 
 

  


 









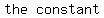
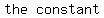
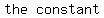
Edwin