Question 1095782: in competiative examination, there were 60 questions, the correct answer would carry 2 marks and for incorrect 1 mark would be subtracted. yash had attempted all the questions and he got total 90 marks. then how many questions he got wrong?
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE FIFTH-GRADER SOLUTION:
With all the answers right, a student would get
 marks. marks.
Each wrong answer makes a student lose  marks, marks,
2 because he did not choose a right answer,
and 1 more because he chose a wrong answer.
A student answered every question and lost  of the possible marks of the possible marks
must have  wrong answers. wrong answers.
He answered the other  questions correctly. questions correctly.
THE ALGEBRA CLASS SOLUTION:
 = number of right answers = number of right answers
 = number of wrong answersin = number of wrong answersin
As all questions were answered,
 . .
The marks for tthe test are

Then, you have to solve the system of linear equations  . .
There are many ways to do that.
COMBINATIONS:
You could do


 

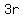   ---> --->  ---> --->
Then you could just substitute that value for  in in 
to get  ---> --->  ---> --->  . .
Otherwise, you could keep doing combinations of equations,
and multiply
 times (-1) to get times (-1) to get  , ,
 times 2 to get times 2 to get  , ,
and add them up to get




    ---> --->  ---> ---> 
Teachers call that adding up of equations a "method" to solve systems of linear equations by making making combinations of the equations, often calling it the "combinations method." Your teacher may use another name.
Why it works and is reasonable:
If 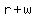 and and  are the same number, are the same number,
and adding the same number to both sides of  we get an equivalent equation, we get an equivalent equation,
we can add 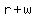 to the left side and to the left side and  to the right side, to the right side,
to get the "combination" equation
 . .
We could also multiply both sides of  times (-2) and add them to times (-2) and add them to 
SUBSTITUTION:
What teachers call "substitution method"
requires solving one of the equations for one of the variables,
and then substituting the expression found into the other equation.
You choose which equation to solve and which variable to solve for.
There are 4 possible choices.
One of them is shown below.
  
      
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
in competiative examination, there were 60 questions, the correct answer would carry 2 marks and for incorrect 1 mark would be subtracted. yash had attempted all the questions and he got total 90 marks. then how many questions he got wrong?
Let number of wrong answers be W
The number of correct answers = 60 - W
We then get the following equation: - 1(W) + 2(60 - W) = 90
Solve this for W, or the number of wrong answers. You should get 10.
That's all. Nothing COMPLEX and/or CONFUSING.
|
|
|