SOLUTION: if 2costheta=x=1/x, 2cosphi=y+1/y,2coslamida=z+1/z,then prove that 2cos(theta+phi+lamida)=xyz+1/(xyz). plz send me ans as early as possible.

1.  If  2*cos(theta) = x + (1/x),  it implies that 


    EITHER  x = 1   and  then  2cos(theta) = 1 + (1/1) = 2  ====>  cos(theta) = 1  ====>  theta = 0,

    OR      x = -1  and  then  2cos(theta) = -1 + (1/(-1)) = -2  ====>  cos(theta) = -1  ====>  theta = .


   It is simply because  x + (1/x) >= 2  if x is positive,  or

                         x + (1/x) <= -2  if x is negative,

   which is  VERY WELL KNOWN fact.



2.  Similarly, from the given data 

    cos(phi) = +/-1      and  phi    = 0     or  phi    =  .

    cos(lambda) = +/-1   and  lambda = 0     or  lambda =  .



3.  Now, if  theta=0,  phi=0  and  lambda=0
         (equivalently, all three cosines are equal to 1)

    then  2cos(theta+phi+lamida)=xyz+1/(xyz)  is, obviously, true.



    Also, if  theta=,  phi=  and  lambda=
         (equivalently, all three cosines are equal to -1)

    then  2cos(theta+phi+lamida)=xyz+1/(xyz)  is, obviously, true, again.


    Finally, if any other combination of possible angles is chosen, 
    it will lead to the same equality, as it is easy to check, having very restricted number of combinations.

The key idea of the solution above is this fact:


    if x is the positive real number, then 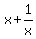  >=2,  
    
    and the equality takes place if and only if  x = 1.


Proof


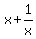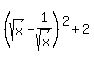 =  is greater than or equal to 2.

The equality takes place if and only if 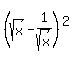  = 0,  which is equivalent to 

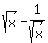 = 0  <=== equivalent to  ===>   =     <=== equivalent to  ===>  x = 1  (under the assumption that x is positive).


The proof is completed.

    Notice.  If you have questions or need more help, you can send a message to me through the "Thank you" form note.

             In this case PLEASE do not forget to refer to the problem ID number, which is  1095761,  
             in order for I could identify the problem.