SOLUTION: Hi! I really find this problem difficult. Hoping someone could help me. Thanks! (X)/(x-3) is greater than (2x-11)/(2x) rational inequality

Algebra ->  Rational-functions -> SOLUTION: Hi! I really find this problem difficult. Hoping someone could help me. Thanks! (X)/(x-3) is greater than (2x-11)/(2x) rational inequality      Log On


   

Question 1095251: Hi! I really find this problem difficult. Hoping someone could help me. Thanks!
(X)/(x-3) is greater than (2x-11)/(2x)
rational inequality
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39625) About Me  (Show Source):
You can put this solution on YOUR website!
Undefined for x at 3 and at x at 0.

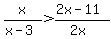x%2F%28x-3%29%3E=%282x-11%29%2F%282x%29
x%2F%28x-3%29-%282x-11%29%2F%282x%29%3E=0
%28x%2A2x-%282x-11%29%28x-3%29%29%2F%282x%28x-3%29%29%3E=0

%282x%5E2-%282x%5E2-11x-6x%2B33%29%29%2F%282x%28x-3%29%29%3E=0

%282x%5E2-2x%5E2%2B17x-33%29%2F%282x%28x-3%29%29%3E=0

%2817x-33%29%2F%282x%28x-3%29%29%3E=0
Critical x values at 3, 0, 33/17.

Check any value in EACH of these intervals to find which intervals are solutions of the inequality:
system%28-infinity%3Cx%3C0%2C0%3Cx%3C=33%2F17%2C33%2F17%3C=x%3C3%2C3%3Cx%3Cinfinity%29

Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

Hi! I really find this problem difficult. Hoping someone could help me. Thanks!
(X)/(x-3) is greater than (2x-11)/(2x)
rational inequality
x%2F%28x+-+3%29+%3E+%282x+-+11%29%2F%282x%29
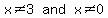Based on the DENOMINATORS, matrix%281%2C3%2C+x+%3C%3E+3%2C+and%2C+x+%3C%3E+0%29
Therefore, we already have 2 critical values: 3 and 0
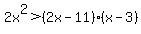2x%5E2+%3E+%282x+-+11%29%28x+-+3%29 ------- Multiplying each side by LCD, (x - 3)(2x)
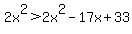
2x%5E2+%3E+2x%5E2+-+17x+%2B+33
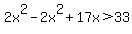2x%5E2+-+2x%5E2+%2B+17x+%3E+33
17x > 33 
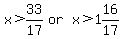matrix%281%2C3%2C+x+%3E+33%2F17%2C+or%2C+x+%3E+1%2616%2F17%29
We now have 3 CRITICAL VALUES: matrix%281%2C6%2C+%223%2C%22%2C+%220%2C%22%2C+and%2C+33%2F17%2C+or%2C+1%2616%2F17%29
There now exists the following 4 (FOUR) INTERVALS that need to be tested.  
==========
Interval 1: x < 0, or x = - 1
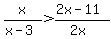
x%2F%28x+-+3%29+%3E+%282x+-+11%29%2F%282x%29
%28-+1%29%2F%28-+1+-+3%29+%3E+%282%28-+1%29+-+11%29%2F%282%28-+1%29%29 ------- Substituting - 1 for x
%28-+1%29%2F%28-+4%29+%3E+%28-+13%29%2F%28-+2%29
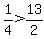Is 1%2F4+%3E+13%2F2? No!! Therefore, a solution DOES NOT exist in this interval.
================
Interval 2: 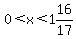0+%3C+x+%3C+1%2616%2F17, or x = 1
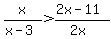
x%2F%28x+-+3%29+%3E+%282x+-+11%29%2F%282x%29
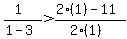%281%29%2F%281+-+3%29+%3E+%282%281%29+-+11%29%2F%282%281%29%29 ------- Substituting 1 for x
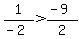1%2F%28-+2%29+%3E+%28-+9%29%2F2
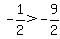Is -+1%2F2+%3E+-+9%2F2? Yes!! Therefore, a solution DOES exist in this interval.
===============
Interval 3: 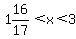1%2616%2F17+%3C+x+%3C+3, or x = 2
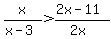
x%2F%28x+-+3%29+%3E+%282x+-+11%29%2F%282x%29
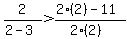2%2F%282+-+3%29+%3E+%282%282%29+-+11%29%2F%282%282%29%29 ------- Substituting 2 for x
2%2F%28-+1%29+%3E+%28-+7%29%2F4
Is -+2+%3E+-+7%2F4? No!! Therefore, a solution DOES NOT exist in this interval.
============
Interval 4: x > 3, or x = 4
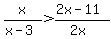
x%2F%28x+-+3%29+%3E+%282x+-+11%29%2F%282x%29
4%2F%284+-+3%29+%3E+%282%284%29+-+11%29%2F%282%284%29%29 ------- Substituting 4 for x
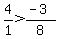4%2F1+%3E+%28-+3%29%2F8
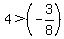Is 4+%3E+%28-+3%2F8%29? Yes!! Therefore, a solution DOES exist in this interval.
The solution, in INTERVAL NOTATION is: