Can someone help?
How to find the term containing x^15y^14 in the expansion of (2x^3+3y^2)^12
Thank you.
The formula to find a SPECIFIC term in a BINOMIAL expansion is:
 , where r = term number
, where r = term number
 ------ Substituting
------ Substituting 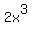 for a,
for a, 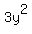 for b, and 12 for n
for b, and 12 for n
 When the above binomial is expanded, the term that contains
When the above binomial is expanded, the term that contains 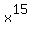 is the one in which:
is the one in which:

 Thus, 15 = 3(13 – r) ------ Bases are equivalent, and so are the exponents
3(5) = 3(13 – r)
5 = 13 – r
5 – 13 = - r
- 8 = - r
r, or term number where
Thus, 15 = 3(13 – r) ------ Bases are equivalent, and so are the exponents
3(5) = 3(13 – r)
5 = 13 – r
5 – 13 = - r
- 8 = - r
r, or term number where 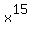 occurs =
occurs =  **Note: If calculated, the 8th term will also contain
**Note: If calculated, the 8th term will also contain 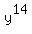 .
.