SOLUTION: Determine the real solutions to the system of nonlinear equations. x^2 + y^2 =4 x^2 + (y+1)^2 = 9 The​ solution(s) is/are __________ ​(Type an ordered pair. Use

Algebra ->  Systems-of-equations -> SOLUTION: Determine the real solutions to the system of nonlinear equations. x^2 + y^2 =4 x^2 + (y+1)^2 = 9 The​ solution(s) is/are __________ ​(Type an ordered pair. Use      Log On


   

Question 1094886: Determine the real solutions to the system of nonlinear equations.
x^2 + y^2 =4
x^2 + (y+1)^2 = 9
The​ solution(s) is/are __________
​(Type an ordered pair. Use a comma to separate answers as needed. Type an exact​ answer, using radicals as​ needed.)
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Both equations contain x%5E2 term.

First step can be %28x%5E2%2B%28y%2B1%29%5E2%29-%28x%5E2%2By%5E2%29=9-4.

Answer by ikleyn(52920) About Me  (Show Source):
You can put this solution on YOUR website!
.
x^2 + y^2 =4
x^2 + (y+1)^2 = 9
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Algebra solution 

You are given

x%5E2+%2B+y%5E2 =4,
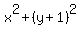x%5E2+%2B+%28y%2B1%29%5E2 = 9


It is the same as

x%5E2+%2B+y%5E2 = 4,                (1)
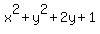x%5E2+%2B+y%5E2+%2B+2y+%2B+1 = 9.           (2)


Subtract equation (1) from equation (2)  (both sides). You will get

2y + 1 = 9-4,  or

2y = 4.                    (3)

Hence, y = 4%2F2 = 2.

Then from (1) you have x = 0.


Answer.  There is one and only one solution  x= 0,  y= 2.


Geometry solution 

Equation (1) represents the circle of the radius 2 centered at the origin of the coordinate system.

Equation (2) represents the circle of the radius 3 centered at the point (0,-1), which lies in the y-axis 1 unit below the origin.

The two circles have only one common point (0,2), where the smaller circle touches the larger circle internally.


So the point (0,2) is the unique solution to the given system of equations.


Regarding the algebra solution, see the lesson
    - Solving systems of algebraic equations of degree 2
on solving similar equations.

Also, you have this free online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this online textbook under the topic "Systems of equations that are not linear".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.