.
Straight line perpendicular to 5x-y = 1 has an equation
5y + x = c, (1)
where c is some (arbitrary) constant.
Our original line has the slope 5; so, the perpendicular line has the slope  and has, therefore,
the equation y =
and has, therefore,
the equation y = 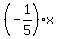 + c, which is of the same form as (1).
So, all you need to do is to determine the constant "c" in equation (1).
For it, notice that straight line (1) has x-intercept (c,0) and y-intercept (0,
+ c, which is of the same form as (1).
So, all you need to do is to determine the constant "c" in equation (1).
For it, notice that straight line (1) has x-intercept (c,0) and y-intercept (0,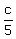 ).
It means, that your right-angled triangle has the legs of
).
It means, that your right-angled triangle has the legs of 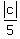 and |c| units long.
Then its area is
and |c| units long.
Then its area is 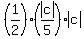 =
=  square units.
You need to have this area equal to 5 square units. It gives you an equation
square units.
You need to have this area equal to 5 square units. It gives you an equation
 = 5,
which implies
= 5,
which implies  = 50 and then c = +/-
= 50 and then c = +/- 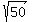 .
It means that you finally have two equations to answer your question
5y + x =
.
It means that you finally have two equations to answer your question
5y + x = 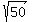 and 5y + x =
and 5y + x = 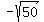 .
.
Solved.