 Factor the first denominator by factoring out 3
Factor the first denominator by factoring out 3
 The LCD is 6(x-2) so we multiply every term
through by
The LCD is 6(x-2) so we multiply every term
through by 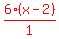
 We cancel whatever will cancel:
We cancel whatever will cancel:
 What we have left is:
What we have left is:


 Get 0 on the right:
Get 0 on the right:
 Multiply through by -1 so x2 term will be positive:
Multiply through by -1 so x2 term will be positive:
 Factor:
Factor:
 5x-2 = 0; x-2 = 0
5x = 2 x = 2
x =
5x-2 = 0; x-2 = 0
5x = 2 x = 2
x =  Two answers are
Two answers are  and
and  .
However, the original problem has denominators that contain
variables. Therefore we must check for extraneous answers
that are not solutions because they cause the denominator to
equal 0. No denominator can ever equal to 0.
The denominators in the original equation are 3x-6 and x-2
Substituting
.
However, the original problem has denominators that contain
variables. Therefore we must check for extraneous answers
that are not solutions because they cause the denominator to
equal 0. No denominator can ever equal to 0.
The denominators in the original equation are 3x-6 and x-2
Substituting  for x in denominator 3x-6 is
for x in denominator 3x-6 is
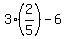

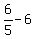

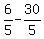

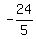 which is not 0
Substituting
which is not 0
Substituting  for x in denominator x-2 is
for x in denominator x-2 is
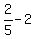

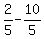

 which is not 0
either, so
which is not 0
either, so  is a solution..
Substituting
is a solution..
Substituting  for x in denominator 3x-6 is
for x in denominator 3x-6 is
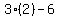

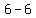

 so we must
discard the answer x = 2, for it is extraneous and is not a
solution. Therefore there is only one solution, x =
so we must
discard the answer x = 2, for it is extraneous and is not a
solution. Therefore there is only one solution, x =  ----------------------------------------
The second one:
----------------------------------------
The second one:
 Add
Add 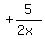 to both sides:
to both sides:
 Since both terms on the right have the same denominator
we can just add the numerators and place it over their
common denominator:
Since both terms on the right have the same denominator
we can just add the numerators and place it over their
common denominator:
 Simplify the right side by dividing top and bottom by 4:
Simplify the right side by dividing top and bottom by 4:
 We could get an LCD as we did in the other one but since
there is only a fraction on each side, we can just
cross-multiply:
We could get an LCD as we did in the other one but since
there is only a fraction on each side, we can just
cross-multiply:

 Get 0 on the right:
Get 0 on the right:

 3x+2 = 0; x-2 = 0
3x = -2; x = 2
x =
3x+2 = 0; x-2 = 0
3x = -2; x = 2
x =  Two answers are
Two answers are  and
and  .
However, the original problem also has denominators that contain
variables. Therefore we must check for extraneous answers
that are not solutions because they cause the denominator to
equal 0. No denominator can ever equal to 0.
The denominators in the original equation are x-1 and 2x.
Substituting
.
However, the original problem also has denominators that contain
variables. Therefore we must check for extraneous answers
that are not solutions because they cause the denominator to
equal 0. No denominator can ever equal to 0.
The denominators in the original equation are x-1 and 2x.
Substituting  for x in denominator x-1 is
for x in denominator x-1 is
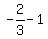

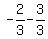

 which is not 0
Substituting
which is not 0
Substituting  for x in denominator 2x is
for x in denominator 2x is
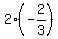

 which is not 0 either, so
which is not 0 either, so
 is a solution.
Substituting
is a solution.
Substituting  for x in denominator x-1 is
for x in denominator x-1 is
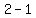

 which is not 0
Substituting
which is not 0
Substituting  for x in denominator 2x is
for x in denominator 2x is
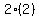

 which is not 0 either, so
which is not 0 either, so
 is also a solution.
So there are two solutions
is also a solution.
So there are two solutions  and 2.
But as you see we must make sure that any answer we get
really is a solution by substituting into each denominator
to show that no answer causes any denominator in the original
equation to be 0.
Edwin
and 2.
But as you see we must make sure that any answer we get
really is a solution by substituting into each denominator
to show that no answer causes any denominator in the original
equation to be 0.
Edwin