Question 1094441: Points R(1, 3), S(–2, –1), and T(5, –1) are vertices of a parallelogram. Give the coordinates of three possible points of the other vertex.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Points 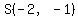 and and  define a horizontal segment ST, define a horizontal segment ST,
with a length of  units. units.
 units to the left of units to the left of 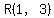 , at U, , at U,
or  units to the right of units to the right of 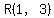 , at V. , at V.
with an x-coordinate of either or or  , ,
and of course the same  as point R. as point R.
So,  and and  are two of the possible locations of the fourth vertex. are two of the possible locations of the fourth vertex.
Those two options give you parallelograms SURT and SRVT, shown below.
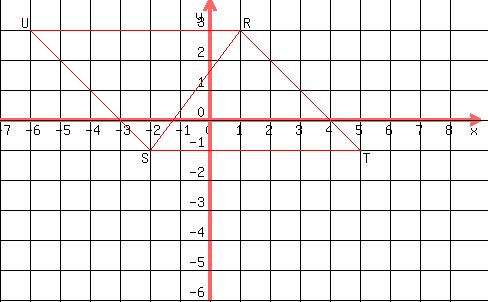 and and 
If ST is a diagonal, then RT and RS are sides,
R is above diagonal ST, and fourth vertex W is below the diagonal
with SW parallel to RT,
SW slanting down from 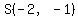 , just as RT slants down from R, , just as RT slants down from R,
going  units down, units down,
and  units to the right. units to the right.
That gives us  , ,
and  , ,
and puts the fourth vertex at 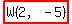 . .
With W, you form parallelogram SWTR, shown below.

|
|
|