|
Question 1094396: Let f(x) = 3x-2 and g(x) = 5/(3x), for x does not equal 0.
Find f^-1(x).
Show that ( g ° f^-1) (x) = 5/(x+2).
Let h(x) = 5/x+2, for x is greater or equal to 0. The graph of h has a horizontal asymptote at y=0.
Find the y-intercept of the graph of h.
Hence, sketch the graph of h.
Find the graph of h^-1, write down the x-intercept.
For the graph of h^-1, write down the equation of the vertical asymptote.
Given that h^-1(a)=3, find the value of a.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let f(x) = 3x-2 and g(x) = 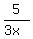 , for x does not equal 0.
Find f-1(x).
1. In place of f(x), replace it by y
y = 3x-2
2. Interchange x and y
x = 3y-2
3. Solve for y
x = 3y-2
3y-2 = x <--swap sides
3y = x+2
y = , for x does not equal 0.
Find f-1(x).
1. In place of f(x), replace it by y
y = 3x-2
2. Interchange x and y
x = 3y-2
3. Solve for y
x = 3y-2
3y-2 = x <--swap sides
3y = x+2
y = 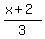 4. In place of y, replace it by f-1(x)
f-1(x) =
4. In place of y, replace it by f-1(x)
f-1(x) = 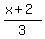 Show that (g∘f-1)(x) =
Show that (g∘f-1)(x) =  .
g(x) = .
g(x) = 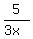 To avoid so many fractions, rewrite using "÷"
g(x) =
To avoid so many fractions, rewrite using "÷"
g(x) =  In place of x, replace it by the right side of f-1(x),
which is {{(x+2)/2}}}
(g∘f-1)(x) =
In place of x, replace it by the right side of f-1(x),
which is {{(x+2)/2}}}
(g∘f-1)(x) =  (g∘f-1)(x) =
(g∘f-1)(x) =  (g∘f-1)(x) =
(g∘f-1)(x) =  (g∘f-1)(x) =
(g∘f-1)(x) = 
Let h(x) =  , for x≧0. The graph of h has a horizontal , for x≧0. The graph of h has a horizontal
asymptote at y=0.
Find the y-intercept of the graph of h.
We let x equal to 0
h(0) = 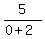 h(0) =
h(0) =  So the y-intercept is the point
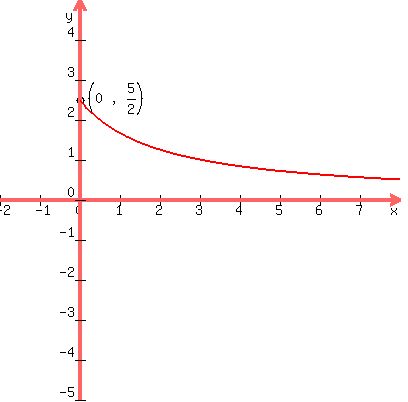
So the y-intercept is the point 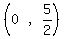 Hence, sketch the graph of h.
Since x≧0, the graph starts at the y-intercept and goes to the
right. The graph does not extend left of the y-intercept:
Hence, sketch the graph of h.
Since x≧0, the graph starts at the y-intercept and goes to the
right. The graph does not extend left of the y-intercept:
 You do the rest by yourself. If you have trouble, tell me in
the thank you note form below, and I will get back to you by
email.
Edwin
You do the rest by yourself. If you have trouble, tell me in
the thank you note form below, and I will get back to you by
email.
Edwin
|
|
|
| |