Question 1094264: |5 x -4| = |x + 17| the 2 soulutions for it
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
|5x -4| = |x + 17| (1)
As you know, the absolute value functions have different expressions in different parts of the number line.
The strategy of solving such problems is to divide the number line in segments/intervals,
where the absolute value functions can be written in more simple way, and then solve the equations over each such interval.
Below find an implementation of this strategy.
There are 2 critical points: x =  and x = -17, and 3 intervals:
(-infinity,-17], (-17, and x = -17, and 3 intervals:
(-infinity,-17], (-17, ) and [ ) and [ ,infinity).
1) Interval (-infinity,-17].
In this interval, 5x-4 < 0; therefore, |5x-4| = -(5x-4).
x + 17 <=0; therefore, |x+17| = -(x+17).
Therefore, the original equation (1) takes the form
-(5x-4) = -(x+17) over the domain x <= -17. (2)
Simplify:
-5x + 4 = -x - 17 ====> 4 + 17 = -x + 5x ====> 4x = 21 ====> x = ,infinity).
1) Interval (-infinity,-17].
In this interval, 5x-4 < 0; therefore, |5x-4| = -(5x-4).
x + 17 <=0; therefore, |x+17| = -(x+17).
Therefore, the original equation (1) takes the form
-(5x-4) = -(x+17) over the domain x <= -17. (2)
Simplify:
-5x + 4 = -x - 17 ====> 4 + 17 = -x + 5x ====> 4x = 21 ====> x =  .
Now notice that this value .
Now notice that this value  does not belong to the domain x <= -17. So, the equation (2) HAS NO solution/solutions over this domain.
Thus this case is completed.
2) Interval (-17, does not belong to the domain x <= -17. So, the equation (2) HAS NO solution/solutions over this domain.
Thus this case is completed.
2) Interval (-17, ).
In this interval, 5x-4 < 0; therefore, |5x-4| = -(5x-4).
x + 17 > 0; therefore, |x+17| = x+17.
Therefore, the original equation (1) takes the form
-(5x-4) = x+17 over the domain -17 < x < ).
In this interval, 5x-4 < 0; therefore, |5x-4| = -(5x-4).
x + 17 > 0; therefore, |x+17| = x+17.
Therefore, the original equation (1) takes the form
-(5x-4) = x+17 over the domain -17 < x <  . (3)
Simplify:
-5x + 4 = x + 17 ====> 4 - 17 = x + 5x ====> 6x = -13 ====> x = . (3)
Simplify:
-5x + 4 = x + 17 ====> 4 - 17 = x + 5x ====> 6x = -13 ====> x = 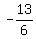 .
This value .
This value 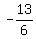 does belong to the domain -17 < x < does belong to the domain -17 < x <  .
So, the equation (3) HAS the solution {{-13/6}}} in this domain.
Hence, it is the solution to the original equation (1), too.
Thus this case is completed.
3) Interval [ .
So, the equation (3) HAS the solution {{-13/6}}} in this domain.
Hence, it is the solution to the original equation (1), too.
Thus this case is completed.
3) Interval [ ,infinity).
In this interval, 5x-4 > 0; therefore, |5x-4| = 5x-4.
x + 17 > 0; therefore, |x+17| = x+17.
Therefore, the original equation (1) takes the form
5x-4 = x+17 over the domain x > ,infinity).
In this interval, 5x-4 > 0; therefore, |5x-4| = 5x-4.
x + 17 > 0; therefore, |x+17| = x+17.
Therefore, the original equation (1) takes the form
5x-4 = x+17 over the domain x >  . (4)
Simplify:
5x-4 = x+17 ====> 5x - x = 17+4 = 21 ====> 4x = 21 ====> x = . (4)
Simplify:
5x-4 = x+17 ====> 5x - x = 17+4 = 21 ====> 4x = 21 ====> x =  .
This value .
This value  does belong to the domain x > does belong to the domain x >  .
So, the equation (4) HAS the solution {{21/4}}} in this domain.
Hence, it is the solution to the original equation (1), too.
Thus this case is completed, too.
Answer. The original equation (1) has two solutions: x = .
So, the equation (4) HAS the solution {{21/4}}} in this domain.
Hence, it is the solution to the original equation (1), too.
Thus this case is completed, too.
Answer. The original equation (1) has two solutions: x = 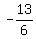 and x = and x =  . .
Solved.

Plot y = |5x-4| (red) and y = |x+17| (green)
---------------
On solving Absolute Value equations see the lessons in this site
- Absolute Value equations
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 2
- HOW TO solve equations containing Linear Terms under the Absolute Value sign. Lesson 3
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 1
- HOW TO solve equations containing Quadratic Terms under the Absolute Value sign. Lesson 2
- OVERVIEW of lessons on Absolute Value equations
Read them attentively and become an expert in this area.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Solving Absolute values equations".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
---------------
WRITING BY @josgarithmetic IS ABSOLUTELY INCORRECT APPROACH TO THE SOLUTION OF THIS PROBLEM.
So, I G N O R E and D I S R E G A R D it.
This person is absolutely unfamiliar with the subject.
|
|
|