SOLUTION: Please help me solve: x(x+2)(x+4)(x+6)+16=0

Algebra ->  Equations -> SOLUTION: Please help me solve: x(x+2)(x+4)(x+6)+16=0      Log On


   

Question 1093850: Please help me solve:
x(x+2)(x+4)(x+6)+16=0
Answer by ikleyn(52794) About Me  (Show Source):
You can put this solution on YOUR website!
.
Introduce new variable  y = x-3  (the central point for the sequence x, x+2, x+4, x+6).


Then your equation takes the form

(y-3)*(y-1)*(y+1)*(y+3) = -16,   or

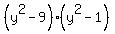%28y%5E2-9%29%2A%28y%5E2-1%29 = -16,

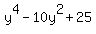y%5E4+-+10y%5E2+%2B+25 = 0,

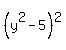%28y%5E2-5%29%5E2 = 0,


which implies  y%5E2 = 5,  and hence  y = +/- sqrt%285%29.


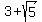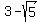Answer.  The original equation has the solutions  x = 3%2Bsqrt%285%29 and  3-sqrt%285%29, each of multiplicity 2.

The lesson to learn from this solution 

    The problem has a hidden symmetry around the central point.
    When written at variables centered at this point, the symmetry becomes explicit and facilitates the problem' solution.