Question 1093836: Solve the equation in [0,2π] by squaring both sides.
Sec x-tanx=-1
Select one:
a. 3π
b. 4π
c. 2π
d. π
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Sec x-tanx=-1
sec = tan - 1
sec^2 = tan^2 - 2tan + 1
tan^2+1 = tan^2 - 2tan + 1
-2tan = 0
tan = 0
x = pi, 2pi
----------
Check for extraneous solutions:
Sec x-tanx=-1
sec(pi) - tan(pi) =? -1
-1 - 0 = -1 OK
=====================
sec(2pi) - tan(2pi) =? -1
1 - 0 = 1 NG
==========================
Only x = pi
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! If the answer must be between  and  ,
 and  are obviously wrong answers.
For  ,  and  ,
so  ,
and  , so  is a solution.
For  ,  too, but  ,
so  , and is not a solution.
IF YOU HAD TO "SHOW YOUR WORK" you would have to solve the equation,
and for that squaring is a reasonable suggestion.
Obviously  is not allowed.
Multiplying times  ,
as long as  ,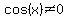
gives an equivalent equation.
Now you can square,
but the resulting equation will have
all the solutions to , and
all the solutions to  ,
so you will have to check for and discard any extraneous solutions.
Squaring, you get
 ,
which can be re-written as
 .
Simplifying and rearranging,
 .
Factoring, gives you
The solutions need to have
 or  .
However,  means ,
and as said at the beginning, that is not allowed.
We are left with ,
which means  .
Checking for extraneous solutions,
we would see that
is a solution of
 ,
and is an extraneous solution.
That leaves us with  ,
which in the interval given happens only when
 .
|
|
|
