.
3sin(x) + 4cos(x) = 5 --->
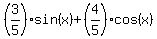 = 1.
Let "a" be the angle in QI such that cos(a) =
= 1.
Let "a" be the angle in QI such that cos(a) =  , sin(a) =
, sin(a) =  .
Such an angle does exists since
.
Such an angle does exists since 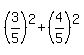 = 1.
Then
1 =
= 1.
Then
1 = 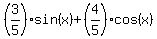 = cos(a)*sin(x) + sin(a)*cos(x) = sin(a+x) = sin(x+a).
It implies that x + a =
= cos(a)*sin(x) + sin(a)*cos(x) = sin(a+x) = sin(x+a).
It implies that x + a =  and, hence, x =
and, hence, x =  , where a =
, where a = 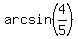
Answer. x = 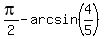 .
.