Question 1093265: Evaluate
1.nC1+2.nC2+3.nC3+...........+n.nCn
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1.nC1 + 2.nC2 + 3.nC3 + ........... +n.nCn
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let S be this sum: S = 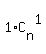 + +  + + 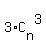 + . . . + + . . . + 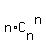 . (1)
Notice that S is the same as
S = . (1)
Notice that S is the same as
S = 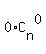 + + 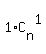 + + 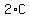 + + 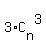 + . . . + + . . . + 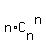 .
Consider 2S and write it in this form
2S = .
Consider 2S and write it in this form
2S = 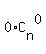 + + 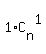 + +  + + 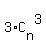 + . . . + + . . . + 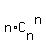 +
+ +
+ 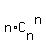 + + 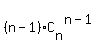 + +  + . . . + + . . . + 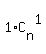 + + 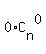 .
Group the terms in pairs combining one term from the upper line and one term from the lower line. You will get
2S = .
Group the terms in pairs combining one term from the upper line and one term from the lower line. You will get
2S = 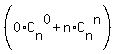 + + 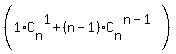 + + 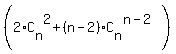 + + 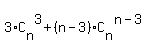 + . . . + + . . . + 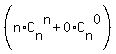 . (2)
Use the fact that . (2)
Use the fact that 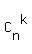 = = 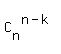 for any k, 0 <= k <= n.
So you can rewrite (2) in the form
2S = for any k, 0 <= k <= n.
So you can rewrite (2) in the form
2S = 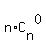 + + 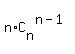 + + 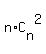 + +  + . . . + + . . . + 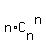 =
= =
= 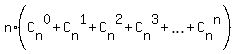 .
Now use well known fact that .
Now use well known fact that
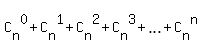 = = 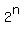 .
Regarding this fact, see the proof in the lesson Remarkable identities for Binomial Coefficients in this site).
Then you finally get
2S = .
Regarding this fact, see the proof in the lesson Remarkable identities for Binomial Coefficients in this site).
Then you finally get
2S =  , and, hence, S = , and, hence, S = 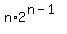 . .
Answer. 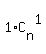 + +  + + 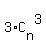 + . . . + + . . . + 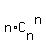 = = 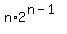 . .
*** Solved ***
----------------
On binomial coefficients see the lessons
- Binomial Theorem, Binomial Formula, Binomial Coefficients and Binomial Expansion
- Remarkable identities for Binomial Coefficients
- The Pascal's triangle
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic
"Binomial expansion, binomial coefficients, Pascal's triangle".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|