Question 1092961: With the lid closed, a takeout box used by a restaurant has a volume of 361 cubic inches. Its length l equals its width w. A strip of tape is wrapped around the box to keep it closed. The length of the tape measures 28 inches, which is 1 inch more than the shortest distance around the box. Find the dimensions of the box.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The more math you know, the more difficult it gets.
THE MIDDLE-SCHOOLER SOLUTION:

If the width and lenth are  , ,
the box volume would be
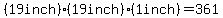   . .
The shape of such a box could work for a small pizza,
but the "shortest distance around the box" would be
 . .
We can also get a volume of 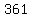  
if we make   and and  . .
Then, the volume in cubic inches is
 . .
In that case, the shortest way around the box is
 , ,
and  . .
So, the solution is
 . .
THE HIGH-SCHOOLER (OR COLLEGE STUDENT) SOLUTION:
We are expected to find all possible solutions,
and "show our work" with equations,
because we already studied algebra,
and maybe even calculus.
We were given  and and 
(for the width and length measuerments of the base/bottom/lid of the box).
We will say that those dimensions are are measured in inches,
and we must define another variable:
 = height of the box in inches. = height of the box in inches.

We must write our equations as
 for the volume, and for the volume, and
 for the length of the tape closing the box. for the length of the tape closing the box.
That may give us more than one solution.
One of the  choices gives us choices gives us
 --> -->  --> -->  --> -->  . .
That solution above is one solution,
but we have to look for any other possible solution.
The other 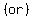 choice gives us choice gives us
 --> -->  --> -->
 --> -->  --> --> 
That  <--> <--> is a cubic equation. is a cubic equation.
I studied polynomial function, so I know that
it must have at least positive real solution for  . .
I may want to use my graphing calculator.
Could there be a rational root?
If there is, it would be of the form  , ,
where  = is a factor of = is a factor of  , ,
and  is a factor of is a factor of  . .
That includes the previously found  . .
Dividing 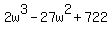 by by 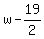 , I get , I get
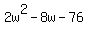 , so the solutions to , so the solutions to 
that work for this problem
are 
and any positive solution to
 <--> <--> . .
I cannot solve that by factoring,
but "completing the square" or using the quadratic formula I find
 , one positive and one negative solution. , one positive and one negative solution.
I could have found the approximate value of 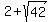 as as 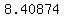 , ,
but the exact 
was probably required.
Then  . .

Am I expected to express that as the exact solution too?

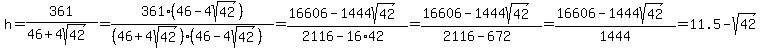
So,

or

is the other solution.
|
|
|