Question 1092649: I need a little help on my homework. I tried them all and I know some of them are right i just have a question on a few because if i can understand those problems the ones similar I can do. So we are learning about how to solve inequalities and graphing them on a number line. I started this one but need a little help finishing it.
(//= absolute value bars)
/x/>x-1, and i need 2 inequalities. i have the first which is x>x-1 but i don't have the other one and is not quite such how to solve either one and my other one is
7-/2x/>5, I have both the inequalities and answers (x>-6; x<6) i just don't know how to put on the third number line because my teacher said something about the union?
Can you help? That would be appreciative?
Found 3 solutions by greenestamps, jim_thompson5910, ikleyn:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
For the first one, yes, you need two inequalities. But one of them is not just
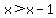
That inequality without absolute value symbols is equivalent to the original inequality only if |x| = x, which is only true if x is 0 or positive.
So you can't just write two inequalities; you need to state when each of the inequalities is true.
If x is 0 or positive, then |x| = x. If x is negative, then |x| = -x. So the correct statement of your two inequalities needs to be
x > x-1, if x >= 0;
-x > x-1, if x < 0
Solving the first inequality gives 0 < 1, which is always true. That means that, in the interval x >=0 where this inequality is applicable, every number is a solution. So the first part of your solution set in interval notation is [0,infinity).
Solving the second inequality leads to 2x < 1, or x < 1/2. This means that any value of x less than 1/2 in the interval where this inequality is applicable is a solution to the original inequality. But every number in this interval (x < 0) is less than 1/2. So every number in the interval where this inequality is applicable is also a solution to the original inequality. So the second part of your solution set in interval notation is (-infinity,0).
Then the complete solution to the original inequality is the union of (-infinity,0) and [0,infinity} -- and in this case that union is all real numbers.
For your second problem, I don't know what two inequalities you have; but the answers are not (x>-6; x<6) -- at least for the original inequality as you show it. Since the variable only appears once in the inequality, there is no need for two equivalent inequalities. The usual solution to you second example would be
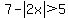
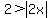
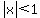
You COULD use two inequalities to separate this into two cases, where x is either negative or positive. However, when the inequality is in this form, it is easiest just to jump directly to the solution,
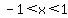 or, in interval notation, (-1,1). or, in interval notation, (-1,1).
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Problem 1) Solve |x| > x-1
If |x| > x-1, then we have two cases:
Case A: x > x-1
OR
Case B: -x > x-1
The difference between case A and case B is that negative out front the first 'x'.
Let's solve for x in each case
Case A:
x > x-1
x-x > x-1-x
0x > 0x - 1
0 > -1
This is always true so we effectively have infinitely many solutions for this inequality. In other words, pick any number you want for x and plug it into the inequality. You will get a true result.
Case B:
-x > x-1
-x+x > x-1+x
0x > 2x-1
0 > 2x-1
2x-1 < 0
2x-1+1 < 0+1
2x+0 < 1
2x < 1
2x/2 < 1/2
x < 1/2
x < 0.5
So any value smaller than 1/2 or 0.5 will work as a solution for this inequality
So to recap, the two solutions are
Case A ---> all real numbers
Case B ---> any real number smaller than 0.5
Since we have the keyword "or" as part of the absolute value definition, this means we combine the two results to get the final answer to be "the set of all real numbers".
We can plug any number in for x, into |x| > x-1, and we'll get a true result. It doesn't matter what number you pick
To graph this, simply draw a number line and shade everything on the number line. This indicates you're including all real numbers.
===============================================================
Problem 2) Solve 7-|2x| > 5
7-|2x| > 5
7-|2x|+|2x| > 5+|2x|
7 > 5+|2x|
7-5 > 5+|2x|-5
2 > |2x|
|2x| < 2
-2 < 2x < 2
-2/2 < 2x/2 < 2/2
-1 < x < 1
To graph this, draw a number line; then plot -1 and 1. Make sure there are open circles at -1 and 1. Finally shade between the open circles (don't shade over the open circles).
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
See the graph below.
The folk wisdom says: It is better to see once, than to hear 100 times.

Plots y = |x| (red) and y = x-1 (green)
The answer to the first your inequality is: the solution is the set of ALL real numbers.
--------------
Solution to the first inequality
|x| > x - 1.
We must re-write this inequality separately for x >= 0 and for x < 0, where the expressions for |x| are different.
1. For x >= 0 you have |x| = x. Then the original inequality takes the form
x > x - 1. (1)
This inequality is true for all values of x.
Thus in the domain x >= 0 the solution for (1), and, hence, for the original inequality is the set [0,infinity).
2. For x < 0 you have |x| = -x. Then the original inequality takes the form
-x > x - 1. (2)
or, equivalently,
2x < 1. ( I hope you know elementary operations with inequalities, so
such transformations should be clear to you . . . )
It implies x < 1/2, which ALWAYS is true in the domain x < 0.
So, in the domain x < 0 the solution set for (2), and, hence, for the original inequality is the set (-infinity,0).
3. Conclusion. The solution set for the original equation is the entire number line.
|
|
|