Question 1092636: Hello, I need help writing this into a tangent function. The only things I have been given are the halfway points and I was not taught how to write a trigonometric function when given those. Thanks in advance for your help!
Write a tangent function, h(x), such that the halfway points on one period are (- pi/2, -2) and (pi/2, 4)
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I have not heard the term "halfway points" for trig functions; but there is only one thing it could mean that makes sense.
One period of the graph of tan(x) is from -pi/2 to pi/2; the period length is pi. The graph of one period is neatly divided into two parts, from -pi/2 to 0 and from 0 to pi/2. If you are talking about the halfway points of a tangent function, the only thing it can mean is the points half way through each half of the graph.
For the graph of the standard tan(x) function between -pi/2 and pi/2, the halfway points of the graph are at x = -pi/4 and x = pi/4; since tan(-pi/4) = -1 and tan(pi/4) = 1, the halfway points are (-pi/4,-1) and (pi/4,1).
Notice that with this meaning of the halfway points, the horizontal distance between the two halfway points is half the period of the function.
Note also that the graph is centered horizontally about x=0 and vertically about y=0.
Now let's look at the halfway points that you are given.
The horizontal difference between the two halfway points is pi; that means the period of the function is 2pi. So our tangent function is going to have a horizontal stretching by a factor of 2.
The two halfway points are equally distant either side of 0, so there is no phase shift. That is fortunate, because the phase shift is the hardest part to figure out in this kind of problem.
And the vertical distance between the halfway points is 6 instead of 2; so we will have a vertical stretch by a factor of 3.
Finally, the graph is no longer centered vertically. The value of the function in the middle of the period -- that is, halfway between the two halfway points -- is the average of the two y values at the halfway points, which is 1. So our function is going to have a vertical shift of +1.
Now we have all the pieces we need to write the function. In the general tangent function
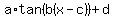
a is the vertical stretch;
b is the horizontal stretch or compression;
c is the phase shift; and
d is the vertical shift
We have determined that the vertical stretch is by a factor of 3; so a is 3.
We have determined that we have a horizontal stretch by a factor of 2; that means b is 1/2. (NOT 2; remember that b>1 indicates a horizontal compression while b<1 means a horizontal stretch.)
We have determined that there is no phase shift, so c=0.
And we have determined that the vertical shift is +1, so d=1.
And we have the desired function:
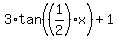
|
|
|