Question 1092505: an object in launched upward at 110 feet per second from a platform 75 feet high .
a) When will the object be 120 feet high?
b) What is its maximum height?
c) When will it reach the ground?
Found 2 solutions by Boreal, rothauserc:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation is -16t^2+110t+75, which accounts for the launch velocity and height.
-16t^2+110t+75=120
-16t^2+110t-45=0; 16t^2-110t+45
t=(1/32)(110+/- sqrt (12100-2880); sqrt 9220=96.02, use 96
t=0..4375 sec and 6.4375 sec. Note, one uses both roots here.
==============
maximum height is at time t=-b/2a=110/32 or 3.44 sec. If I use exact answer or 3.4375 the height is 264.0625 feet, 264 feet. If I use 3.44 sec the height is 264 feet.
=============
hits ground when 16x^2-110x-75=0
x^2-110x-1200=0 divide first term by 16 and multiply last by 16
(x-120)(x+10)=0
divide constants by 16 and reduce to lowest terms
(x-(15/2))(x+(5/8))=0
move the denominator out front
(2x-15)(8x+5)=0
Postitive root is x=7.5 seconds.

Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! the height of the object at time t is modeled by the following formula
:
s(t) = –gt^2 + v0t + h0, where g is the acceleration due to gravity, v0 is the objects initial velocity, h0 is the initial height of the object
:
since we are working in feet, g=16, also v0=110 and h0=75
:
s(t) = -16t^2 +110t +75
:
this is a parabola that curves downward
:
the graph of this equation is
:
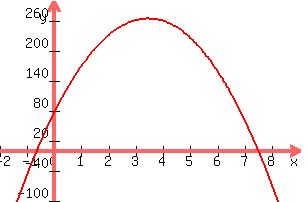
:
a) 120 = -16t^2 +110t +75
-16t^2 +110t -45 = 0
t^2 -6.875t +2.8125 = 0
use quadratic formula to solve for t
t = (-(-6.875) +square root((-6.875)^2 -4(1)(2.8125))) / 2(1) = 6.4382 seconds
t = (-(-6.875) -square root((-6.875)^2 -4(1)(2.8125))) / 2(1) = 0.4368 seconds
Note that the object attains the height of 120 feet at two different times(on the way up and again on the way down)
:
b) t = -b/2a(this is the t value associated with the vertex)
s(t) = -16t^2 +110t +75
t = -110 / 2(-16) = 3.4375
s(3.4375) = -16(3.4375)^2 +110(3.4375) +75 = 264.0625 feet at its maximum height
:
c) s is 0 when the object hits the ground
0 = -16t^2 +110t +75
t^2 -6.875t -4.6875 = 0
t = (-(-6.875) +square root((-6.875)^2 -4(1)(-4.6875))) / 2(1) = 7.5
t = (-(-6.875) +square root((-6.875)^2 -4(1)(-4.6875))) / 2(1) = -0.625
we reject the negative value for t, therefore the object hits the ground after 7.5 seconds
:
|
|
|