Question 1092417: A. Find the limit of f(x) = x - 2 / x^2 - 3x + 2 as x approaches 1, or explain why the limit does not exist.
B. Find the limit of f(x) = x - 2 / x^2 - 3x + 2 as x approaches 2, or explain why the limit does not exist.
C. Apply the definition of continuity to identify any points of discontinuity in the function f, showing all work. 1. Explain the effect of the discontinuities identified in part C on the domain and range of the function f.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The given function can be written as
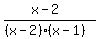
If x is not 2 (so that x-2 is not 0), then we can divide numerator and denominator by (x-2); so everywhere except at x=2, this function is the same as the function
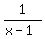
That is enough to answer part B of your question. Except at x=2, the function is everywhere the same as the function 1/(x-1); that means that as you approach 2 from either direction, the function value is getting closer and closer to the value of 1/(x-1) at x=2, which is 1. Since you approach the same value from either direction, the limit exists at x=2; the limit is 1.
Everywhere except at x=2, the function is the same as 1/(x-1). To see if the limit exists at x=1, look what happens when you approach x=1 from the left or the right.
If you are approaching from the left, x is less than 1; as you get very close to 1 from the left, (x-1) is negative and gets very close to 0. That makes the value of 1/(x-1) a large negative number. So the limit as you approach x=1 from the left is negative infinity.
But when you approach x=1 from the right, (x-1) becomes a very small positive number, so 1/(x-1) becomes a very large positive number. So the limit as you approach x=1 from the right is positive infinity.
Since the limits as you approach x=1 from the two directions are different, the limit does not exist at x=1.
So the function is discontinuous at x=1 and x=2; in fact, we knew that would be the case in the beginning, since the denominator of the function factors as (x-2)(x-1).
Obviously, since the denominator can't be 0, the points x=1 and x=2 are excluded from the domain; all other values of x are allowed.
We know that the limit as x approaches 2 from either direction is 1. To see if there are any restrictions on the range, we need to see if there are any x values for which the function value is 1.



The only value of x for which the function value is 1 is x=2, which is not in the domain of the function. That means there is no value of x for which the y value is 1. So the range of the function is all real numbers except 1.
|
|
|