SOLUTION: Determine the value of m so that when f(x) is divided by (x-4) the remainder is -8. f(x)=3x^2+mx+4

There are two ways to do this problem.

Method 1:

The remainder theorem states: 

When a polynomial f(x) is divided by (x-r), the remainder is f(r).

Therefore f(4) = -8

 3(4)² + m(4) + 4 = -8
   3(16) + 4m + 4 = -8
      48 + 4m + 4 = -8
          52 + 4m = -8
               4m = -60
                m = -15

Method 2:

You can also do it by synthetic division

4 | 3       m         4
  |        12     4(m+12)
    3     m+12   4+4(m+12)

Then set the remainder equal to -8

         4+4(m+12) = -8
           4+4m+48 = -8
             52+4m = -8
                4m = -60
                 m = -15

Edwin

According to the Remainder theorem, 


    if  f(x) gives the remainder -8  when is divided by (x-4),  then the value f(4) is equal to -8:  f(4) = -8.



So, from the condition, you have THIS  equation to find m:

    3*4^2 +m*4 + 4 = -8.


Simplify and solve for m:

    3*16 + 4m + 4 = -8  ====>  4m = -3*16 - 4 - 8  ====>  4m = -60  ====>  m = 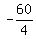 = -15.


Answer.  m = -15.

    Theorem   (the remainder theorem)

    1. The remainder of division the polynomial    by the binomial    is equal to the value    of the polynomial. 

    2. The binomial    divides the polynomial    if and only if the value of    is the root of the polynomial  ,  i.e.  .

    3. The binomial    factors the polynomial    if and only if the value of    is the root of the polynomial  ,  i.e.  .