SOLUTION: Primal Problem: maximize profit P = 40x + 30y constraints: 1. x + y <= 240 2. 2x + y <= 320 x >= 0, y >= 0 I need the answer by DUAL SIMPLEX METHOD..??

Actually the DUAL Simplex method is for minimizing, not
maximizing.  So we do not use the DUAL here but the
regular Simplex method.

Maximize profit  subject to

 

Then non-negative slack variables ,  are
introduced to turn the inequalities into equations and the
objective function equation is rearranged at the bottom with
0 on the right side:



Then it is written as



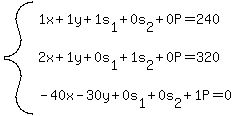And this system of equations is written as an augmented matrix:



The most negative number (indicator) on the bottom row is -40.  
It is in column 1, so column 1 is the PIVOT COLUMN

We now divide each of the positive numbers above the pivot element
-40 INTO the element at the far right of its row:

    240             160
  1)240           2)320

The smallest of 240 and 160 is 160, which was gotten using the elements
of row 2, so row 2 is the PIVOT ROW.

So the element in the PIVOT ROW and the PIVOT COLUMN is the 2,
which is called the PIVOT ELEMENT, boxed in red below.



We make the pivot element into a 1 by dividing the entire pivot row through
by 2.



Now we make all the other numbers in the pivot column 0 by using this
pivot row, multiplying it by whatever is necessary to multiply it by so
that when we add it to the other row its first element will be 0.

We make the 1 in the 1st row 1st column a 0 by multiplying the 2nd
row (the pivot row) temporarily by -1 and adding it to row 1.



We make the -40 in the bottom row 1st column a 0 by multiplying the 2nd
row temporarily by 40 and adding it to row 3.




-----
The most negative number (indicator) on the bottom row is -10.  
It is in column 2, so now column 2 is the new PIVOT COLUMN

We now divide each of the positive numbers above the -10 INTO the
element at the far right of its row.  So we divide 80 by 1/2,
and 160 by 1/2. 

80÷(1/2) = 80×(2/1) = 160
10÷(1/2) = 160×(2/1) = 320

The smallest of 160 and 320 is 160, which was gotten using the elements
of row 1, so row 1 is the new PIVOT ROW.

So the element in the PIVOT ROW and the PIVOT COLUMN is the 1/2,
which is called the PIVOT ELEMENT, boxed in red below.



We make the pivot element into a 1 by dividing the entire pivot row through
by 1/2, which is the same as multiplying it by 2:



Now we make all the other numbers in the pivot colomn 0 by using this
pivot row, multipling it by whatever is necessary to multiply it by so
that when we add it to the other row its first element will be 0.

We make the 1/2 in the 2nd row 2nd column a 0 by multiplying the 1st
row (the pivot row) temporarily by -1/2 and adding it to row 2.




We make the -10 in the 3rd row 2nd column a 0 by multiplying the 1st
row temporarily by 10 and adding it to row 3.



Now there are no more negative numbers on the bottom row. So we
write the matrix as a system of equations:



Eliminate the zero terms and the 1 coefficients:



Now solve the bottom equation for P, the letter to maximize:



Since  and  are non-negative,
the maximum value P can take on is 8000, when  and 
 are both 0, so we substitute 0 for  and 


and the system becomes:






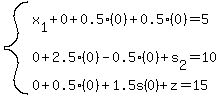
or



So P reaches the maximum value of  when 
 and .  And
of course the slack variables  and .

Edwin