SOLUTION: The Numerator of a fraction is increase by 8 and the denominator is decreased by 1, the resulting fraction is the reciprocal of the original fraction. What is the original fraction

Algebra ->  Rational-functions -> SOLUTION: The Numerator of a fraction is increase by 8 and the denominator is decreased by 1, the resulting fraction is the reciprocal of the original fraction. What is the original fraction      Log On


   

Question 1092151: The Numerator of a fraction is increase by 8 and the denominator is decreased by 1, the resulting fraction is the reciprocal of the original fraction. What is the original fraction? (Please provide the complete solution) Thank you.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216) About Me  (Show Source):
You can put this solution on YOUR website!

Interesting problem. I thought it would be easy to solve algebraically, but I don't see a purely algebraic solution. I will be interested to watch and see if someone has one for you.

It seems simple enough. If n and d are the numerator and denominator of the original fraction, then you want

%28n%2B8%29%2F%28d-1%29+=+d%2Fn

But when you try to solve that using standard algebraic processes, what you get is
n%28n%2B8%29+=+d%28d-1%29

you could rewrite this as
n%5E2%2B8n+=+d%5E2-d

But that doesn't help any. We have one equation with two unknowns. That suggests Diophantine equations; but I don't know procedures for solving quadratic Diophantine equations.

So I can find AN answer (I haven't been able to see why there couldn't be others) by plugging in values for n and seeing if the product n(n+8) is a number I recognize as being the product of two consecutive integers.

It happens rather quickly. Trying n=1 gives n(n+8)=9; that doesn't work. But trying n=2 gives n(n+8) = 20, which I immediately recognize as 5*4.

So "A" solution to your problem is that the numerator is 2 and the denominator is 5.

The solution 2/5 can be seen to work:
%28n%2B8%29%2F%28d-1%29+=+10%2F4+=+5%2F2
which is the reciprocal of 2/5.

Answer by ikleyn(52915) About Me  (Show Source):
You can put this solution on YOUR website!
.
The basic equation is

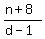%28n%2B8%29%2F%28d-1%29 = d%2Fn.

It implies after cross multiplying

n^2 + 8n = d^2 -d  ====>

n^2 - d^2 = -8n - d  ====>

(n+d)*(n-d) = -8n - d  ====>

(n+d)*(d-n) = 8n + d  ====>

(n+d)*(d-n) = (8n - 8d) + (8d + d)  ====>

(n+d)*(d-n) = -8*(d-n) + 9d  ====>  divide both sides by (d-n)  ====>

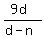n + d = -8 + %289d%29%2F%28d-n%29.   (1)


     By the way (as an aside notice) it follows from the last formula that d > n.


Now, from the very beginning we can assume that our ratio/fraction is  just REDUCED, so n and d have no common factors 
and are relatively prime numbers.

Then "d" and "d-n" in (1) are relatively prime TOO.

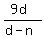Then, since  %289d%29%2F%28d-n%29  in (1) is an integer number,  it implies that (d-n) divides 9.


So, the only possible cases are

    a) d-n = 1;
    b) d-n = 3;
    c) d-n = 9.


Case a) d-n = 1 implies (through (1)) that  n+d = -8 + 9d. Then you have this system of two eqns 
                d-n = 1  and  n+d = -8+9d. It has the only solution n=0, d=1, which DOESN't work.


case b) d-n = 3 implies (through (1) )  n+d = -8 + %289%2Ad%29%2F3 = -8+3d. Then you have this system of two eqns  
                d-n = 3 and n+d = -8+3d.  It has the only solution n=2, d=5. 

                It is the case found by @greenestamps


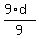Case c) d-n = 9 implies (through (1) ) n+d = -8 + %289%2Ad%29%2F9 = -8+d.  Then you have this system of two eqns 
                d-n = 9  and  n+d = -8+d.
                It has the only solution n= -8, d= 1, which DOESN't work.

Thus the only solution is  n = 2,  d = 5  with the fraction  2/5  =  2%2F5.


            **************
            *** SOLVED ***
            **************


Now I can sign this work proudly: IKleyn, MekhMat MGU (= MSU) 1965/70, PhD in Physics and Mathematics.