.
The third term of an arithmetic sequence is 8 and the sixth term is 2. Find the 30th term
~~~~~~~~~~~~~~~~~
 = 8 =
= 8 = 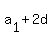 . (1) (
. (1) ( is the first term of the AP)
is the first term of the AP)
 = 2 =
= 2 = 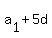 . (2) (d is the common difference of the AP)
Subtract eqn(1) from eqn(2). You will get
5d - 2d = 2 - 8, or 3d = -6. Hence, d =
. (2) (d is the common difference of the AP)
Subtract eqn(1) from eqn(2). You will get
5d - 2d = 2 - 8, or 3d = -6. Hence, d = 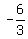 = -2.
Now
= -2.
Now  =
= 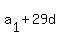 =
= 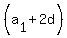 +
+  =
= 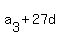 = 8 + 27*(-2) = 8 - 54 = -46.
Answer.
= 8 + 27*(-2) = 8 - 54 = -46.
Answer.  = -46.
= -46.
Solved.
To confirm my solution, I prepared this Table in Excel on my computer.
n  ---------------
1 I do not need the terms
---------------
1 I do not need the terms  and
and  ,
2 so I left these cells empty.
3 8
4 6
5 4
6 2
7 0
8 -2
9 -4
10 -6
11 -8
12 -10
13 -12
14 -14
15 -16
16 -18
17 -20
18 -22
19 -24
20 -26
21 -28
22 -30
23 -32
24 -34
25 -36
26 -38
27 -40
28 -42
29 -44
30 -46
,
2 so I left these cells empty.
3 8
4 6
5 4
6 2
7 0
8 -2
9 -4
10 -6
11 -8
12 -10
13 -12
14 -14
15 -16
16 -18
17 -20
18 -22
19 -24
20 -26
21 -28
22 -30
23 -32
24 -34
25 -36
26 -38
27 -40
28 -42
29 -44
30 -46
-------------------
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.