Question 1091801: One leg of a right triangle has a length of 11 and all sides are whole numbers. Find the lengths of the other two sides and the hypotenuse?
Found 2 solutions by jorel1380, ikleyn:
Answer by jorel1380(3719)   (Show Source): (Show Source):
You can put this solution on YOUR website! We can use the formulas a = x 2 – y 2, b = 2xy, c = x 2 + y 2 to answer this question. Let the legs of the right triangle be a and b and the hypothenus be c, then by the pythagoras theorem
a^2+b^2=c^2
Given that
a =x^2-y^2
Let a = 11, then
x^2-y^2=11
By trial and error, we can find that the value of x = 6 and the value of y = 5.
i.e.
x^2-y^2=6^2-5^2=36-25=11
Thus,
b = 2(6)(5) = 60
and
x^2+y^2=6^2+5^2=36+25=61
Therefore, the other leg = 60 and the hypotenuse = 61.
☺☺☺☺
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One leg of a right triangle has a length of 11 and all sides are whole numbers. Find the lengths of the other two sides and the hypotenuse?
~~~~~~~~~~~~~~~~~~~~
I read the solution by @jorel1380's and, to be honest, did understand NOTHING.
My feeling is that this solution is wrong. Although the answer is correct.
Below please find the correct solution.
From the Pythagorean theorem we have
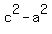 = =  ,
or, applying the formula for square difference,
(c-a)*(c+a) = ,
or, applying the formula for square difference,
(c-a)*(c+a) =  .
The left side is the product of two positive integer numbers. The right side is a square of a prime number.
It follows from the Fundamental Theorem of Arithmetic (theorem on unique decomposition of any integer into the product of prime numbers)
that one and only one of two alternatives takes place.
1. EITHER
c + a = 11,
c - a = 11,
2. OR
c + a = 121,
c - a = 1.
The alternative 1 implies a = 0, therefore, it is excluded.
The alternative 2 implies (after adding the two equation) that
2c = 122 ===> c = .
The left side is the product of two positive integer numbers. The right side is a square of a prime number.
It follows from the Fundamental Theorem of Arithmetic (theorem on unique decomposition of any integer into the product of prime numbers)
that one and only one of two alternatives takes place.
1. EITHER
c + a = 11,
c - a = 11,
2. OR
c + a = 121,
c - a = 1.
The alternative 1 implies a = 0, therefore, it is excluded.
The alternative 2 implies (after adding the two equation) that
2c = 122 ===> c = 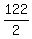 = 61.
Then as the next easy step you find a = 60. = 61.
Then as the next easy step you find a = 60.
So, the answer is 61 for the hypotenuse and 60 for the longer leg.
Solved.
--------------
As a conclusion, I want to say, addressing to the tutors:
The problems like this - they are not routine school math - require very careful treatment,
because they have educational impact to students.
So, EITHER you can solve and present a solution brilliantly, - and then your contribution is positive,
OR you can not do it in this manner - and then your contribution is negative.
Notice: not ZERO contribution, but NEGATIVE, because the student will not obtain that positive charge and charm that the problem
really carries itself.
Instead he or she will get the portion of disgusting and the portion of hate to Math.
|
|
|